题目内容
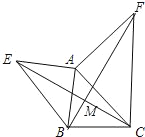
【题目】如图,正方形ABCD的边长为1,E是AD边上一动点,AE=m,将△ABE沿BE折叠后得到△GBE.延长BG交直线CD于点F. 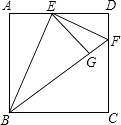
(1)若∠ABE:∠BFC=n,则n=;
(2)当E运动到AD中点时,求线段GF的长;
(3)若限定F仅在线段CD上(含端点)运动,直接写出m的取值范围.
【答案】
(1)1:2
(2)解:当E运动到AD中点时,AE=DE= ![]() ,
,
由折叠得,DE=GE,∠EGF=∠D=90°,BG=AB=1,
根据DE=GE,EF=EF可得,Rt△EDF≌Rt△EGF(HL),
∴DF=GF,
设DF=GF=x,则CF=1﹣x,
∵在Rt△BCF中,BC2+FC2=BF2,
∴12+(1﹣x)2=(1+x)2,
解得x= ![]() ,
,
∴线段GF的长为 ![]() ;
;
(3)解:若限定F仅在线段CD上(含端点)运动,则
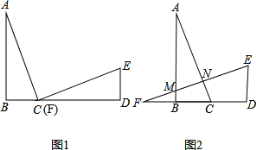
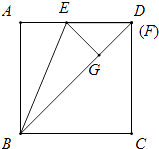
①如图,当点F与点D重合时,AE=EG=GF=m,FE=1﹣m,
在Rt△EFG中,m2+m2=(1﹣x)2,
解得m=﹣ ![]() ﹣1(舍去),m=
﹣1(舍去),m= ![]() ﹣1;
﹣1;
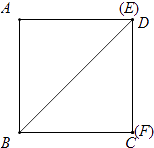
②如图,当点F与点C重合时,点E与点D重合,此时AE=AD=1,
∴m=1.
综上,m的取值范围是: ![]() ﹣1≤m≤1.
﹣1≤m≤1.
【解析】 解:(1)∵正方形ABCD中,AB∥CD,
∴∠ABF=∠BFC,
由折叠得,∠ABF=2∠ABE,
∴∠BFC=2∠ABE,
∴∠ABE:∠BFC=1:2,
∴n=1:2,
故答案为:1:2;
(1)根据正方形的性质可得∠ABF=∠BFC,根据折叠可得∠ABF=2∠ABE,由此得出n的值即可;(2)先根据折叠的性质,判定Rt△EDF≌Rt△EGF,再设DF=GF=x,在Rt△BCF中运用勾股定理求得x的值即可;(3)若限定F仅在线段CD上(含端点)运动,则分两种情况进行讨论:点F与点D重合,点F与点C重合,进而求得m的取值范围.