题目内容
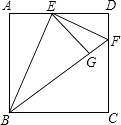
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.试判断线段EC与BF的关系并证明.
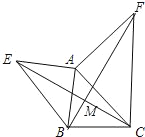
【答案】EC=BF; EC⊥BF,证明见解析.
【解析】
先由条件可以得出∠EAC=∠BAE,再证明△EAC≌△BAF就可以得出结论.
EC=BF; EC⊥BF,理由如下:
证明:∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF,
在△ABF和△AEC中,
∵AE=AB,∠EAC=∠BAF,AF=AC,
∴△ABF≌△AEC(SAS),
∴EC=BF;∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,
∴EC⊥BF.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目