题目内容
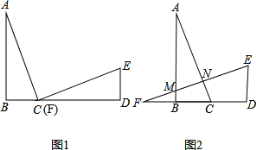
【题目】已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AC=EF,BC=DE .
(1)请说明△ABC≌△FDE,并判断AC是否垂直FE?
(2)若将△ABC 沿BD方向平移至如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么?
【答案】(1)AC⊥EF,理由见解析; (2)AC⊥FE,理由见解析.
【解析】
(1)根据HL的判定方法可证明△ABC≌△FDE,根据两个全等直角三角形的几个锐角之间的关系即可证明AC⊥EF.(2)由(1)可知∠A=∠F,根据∠ABC=∠ABF=90°,∠AMN=∠FMB,可知∠F+∠FMB=90°, ∠A+∠AMN=90°,进而可证明∠ANM=90°,即AC⊥FE.
(1)AC⊥EF.理由如下:
∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△FDE中
∵AC=EF,BC=DE
∴△ABC≌△FDE(HL)
∴∠A=∠EFD,
∵∠B=90°,
∴∠A+∠ACB=90°,
∴∠ACB+∠ECD=90°,
∴∠ACE=180°-90°=90°,
∴AC⊥CE,
即AC⊥FE.
(2)AC垂直FE,理由如下:
∵∠A=∠F(已证),∠ABC=∠ABF=90°,∠AMN=∠FMB,
∴∠F+∠FMB=90°,
∴∠A+∠AMN=90°,
∴∠ANM=180°-90°=90°,
∴AC⊥FE.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目