题目内容
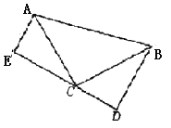
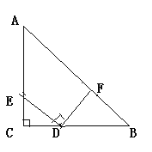
【题目】如图,已知在△ABC中,AD⊥BC于点D,BE⊥AC于点E,且DF=DC。
(1)求证:BD=AD;
(2)若AF=1,DC=3,求BF的长.
【答案】(1)证明见解析;(2)BF=5
【解析】
(1)、根据AD⊥BC和AC⊥BE得出∠EBC+∠C=90° ,∠CAD+∠C=90°,从而得出∠CAD=∠EBC,结合DF=DC得出△ACD和△BFD全等,从而得出答案;(2)、根据全等得出AF=1,DC=3,DF=DC,BD=AD=4,最后根据Rt△ADC的勾股定理求出AC的长度,即BF的长度.
(1)证明:∵ AD⊥BC,
∴ △ACD和△BFD是直角三角形 (两边相互垂直的三角形是直角三角形),∵ AC⊥BE,
∴ ∠BEC=90°,∴ ∠EBC+∠C=90°,∵ △ACD是直角三角形,
∴ ∠CAD+∠C=90° (直角三角形的两个锐角互余),
∵ ∠EBC+∠C=90° ,∠CAD+∠C=90°,∴ ∠CAD=∠EBC,∴ △ACD≌△BFD(AAS),
∴ BD=AD(全等三角形的对应边相等),
(2)、由(1)得△ACD≌△BFD, ∴BD=AD,AD=AC(全等三角形的对应边相等),
∵AF=1,DC=3,DF=DC, ∴BD=AD=4,又∵AD⊥BC,
∴AD2+DC2=AC2(勾股定理), ∴BF=AC=5.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目