题目内容
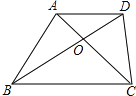
【题目】(1)如图1,在ABCD中,对角线AC与BD相交于点O,△AOB是等边三角形,AB=4,求ABCD的面积.
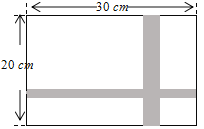
(2)如图2,在△ABC中,∠B=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长(结果保留根号)

【答案】(1)16![]() (2)2
(2)2![]() +2
+2
【解析】
(1)首先证明S平行四边形ABCD=4S△ABO,求出等边三角形△ABO的面积即可;
(2)由题意BD=BC,设BD=BC=x,根据AB=![]() BC,构建方程即可解决问题;
BC,构建方程即可解决问题;
(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴S平行四边形ABCD=4S△ABO,
∵△ABO是等边三角形,AB=4,
∴S△ABO=![]() ×42=4
×42=4![]() ,
,
∴S平行四边形ABCD=16![]() .
.
(2)∵∠BDC=45°,∠B=90°,
∴BD=BC,设BD=BC=x,
在Rt△ABC中,∵∠A=30°,
∴AB=![]() BC,
BC,
∴4+x=![]() x,
x,
∴x=2![]() +2,
+2,
∴BC=2![]() +2.
+2.

练习册系列答案
相关题目
【题目】2020年日本奥运会的比赛门票开始接受公众预订.下表为日本奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷准备用8000元预订10张下表中比赛项目的门票.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票,问他可以订男篮门票和乒乓球门票各多少张?
(2)若在现有资金8000元允许的范围内和总票数不变的前提下,他想预订下表中三种球类门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,求他能预订三种球类门票各多少张?