Question

【题目】已知正方形ABCD的边长为4，一个以点A为顶点的45°角绕点A旋转，角的两边分别与BC、DC的延长线交于点E、F，连接EF，设CE=a，CF=b．

（1）如图1，当a=4时，求b的值；

（2）当a=4时，如图2，求出b的值；

（3）如图3，请写出∠EAF绕点A旋转的过程中a、b满足的关系式，并说明理由．

Answer 1

【答案】（1）4（2）8（3）32

【解析】

（1）先判断出∠ACF=∠ACE，再判断出∠CAF=∠CAE，进而判断出△ACF≌△ACE，即可得出结论；

（2）先判断出∠AFC+∠CAF=45°，判断出∠CAF=∠AEC，进而判断出△ACF∽△ECA，即可得出结论；

（3）（2）已证．

（1）∵四边形ABCD是正方形，

∴∠BCF=∠DCE=90°

∵AC是正方形ABCD的对角线，

∴∠ACB=∠ACD=45°，

∴∠ACF=∠ACE，

∵AC是边长为4的正方形的对角线，

∴∠CAD=45°，AC=4，

∵a=CE=4，

∴AC=CE，

∴∠CAE=∠BEA，

∵四边形ABCD是正方形，

∴AD∥BC，

∴∠DAE=∠BEA，

∴∠CAE=∠DAE=∠CAD=22.5°，

∵∠EAF=45°，

∴∠CAF=∠EAF﹣∠CAE=22.5°=∠CAE，

在△ACF和△ACE中，

，

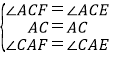∴△ACF≌△ACE，

∴b=CF=CE=4，

（2）∵AC是正方形ABCD的对角线，

∴∠BCD=90°，∠ACB=45°，

∴∠ACF=180°，

∴∠AFC+∠CAF=45°，

∵∠AFC+∠AEC=180°﹣（∠CFE+∠CEF）﹣∠EAF=180°﹣90°﹣45°=45°，

∴∠CAF=∠AEC，

∵∠ACF=∠ACE=135°，

∴△ACF∽△ECA，

∴，

∴EC×CF=AC2=2AB2=32

∴ab=32，

∵a=4，

∴b=8；

（3）ab=32，

理由：（2）已证．