جâؤ؟ؤعبف
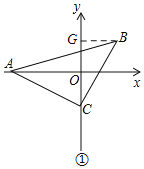
،¾جâؤ؟،؟بçح¼£¬،÷ABCتاµبرüض±½اب½اذخ£¬،دBCA£½90،م£¬BC£½AC£¬ض±½ا¶¥µمCشعyضلةد£¬بٌ½ا¶¥µمAشعxضلةد£®

£¨1£©بçح¼¢ظ£¬بôµمCµؤ×ّ±êتا£¨0£¬©پ1£©£¬µمAµؤ×ّ±êتا£¨©پ3£¬0£©£¬اَBµمµؤ×ّ±ê£»
£¨2£©بçح¼¢ع£¬بôxضلا،؛أئ½·ض،دBAC£¬BCسëxضل½»سعµمD£¬¹µمB×÷BE،حxضلسعE£¬ختADسëBEسذشُرùµؤتء؟¹طدµ£¬²¢ثµأ÷ہيسة£»
£¨3£©بçح¼¢غ£¬ض±½ا±كACشعء½×ّ±êضلةد»¬¶¯£¬ت¹µمBشعµعثؤدَدقؤع£¬¹Bµم×÷BF،حxضلسعF£¬شع»¬¶¯µؤ¹³جضذ£¬²آدëOC،¢BF،¢OAض®¼نµؤ¹طدµ£¬²¢ض¤أ÷ؤمµؤ½لآغ£®
،¾´ً°¸،؟£¨1£©B£¨1£¬2£©£»£¨2£©AD£½2BE£¬ہيسة¼û½âخِ£»£¨3£©OC£½BF+OA£¬ہيسة¼û½âخِ
،¾½âخِ،؟
£¨1£©£©بçح¼¢ظ£¬¹B×÷BG،حyضلسعG£¬ض¤أ÷،÷AOC،ص،÷CGB£¨AAS£©£¬µأAO=CG=3£¬OC=BG=1£¬±يت¾µمBµؤ×ّ±ê£»
£¨2£©بçح¼¢ع£¬رس³¤BE،¢AC½»سعH£¬ض¤أ÷،÷AEB،ص،÷AEH£¨ASA£©£¬µأBE=EH£¬¼´BH=2BE£¬شظض¤أ÷،÷ACD،ص،÷BCH£¨ASA£©£¬؟ةµأ½لآغ£»
£¨3£©بçح¼¢غ£¬¹C×÷CM،حBF£¬½»FBµؤرس³¤دكسعM£¬ض¤أ÷،÷AOC،ص،÷BMC£¨AAS£©£¬ثؤ±كذخOCMFخھ¾طذخ£¬¸ù¾فدك¶خµؤ؛ح؟ةµأ½لآغ£®
£¨1£©بçح¼¢ظ£¬¹B×÷BG،حyضلسعG£¬
،كµمCµؤ×ّ±êتا£¨0£¬©پ1£©£¬µمAµؤ×ّ±êتا£¨©پ3£¬0£©£¬
،àOC£½1£¬OA£½3£¬
،ك،دBCA£½90،م£¬
،à،دACO+،دBCG£½90،م£¬
،ك،دBCG+،دCBG£½90،م£¬
،à،دACO£½،دCBG£¬
،كAC£½BC£¬،دAOC£½،دBGC£½90،م£¬
،à،÷AOC،ص،÷CGB£¨AAS£©£¬
،àAO£½CG£½3£¬OC£½BG£½1£¬
،àOG£½3©پ1£½2£¬
،àB£¨1£¬2£©£»
£¨2£©بçح¼¢ع£¬AD£½2BE£¬
ہيسةتا£؛رس³¤BE،¢AC½»سعH£¬

،كBE،حxضل£¬
،à،دAEB£½،دAEH£½90،م£¬
،كAEئ½·ض،دBAC£¬
،à،دCAD£½،دBAD£¬
،كAE£½AE£¬
،à،÷AEB،ص،÷AEH£¨ASA£©£¬
،àBE£½EH£¬¼´BH£½2BE£¬
،ك،دACD£½،دBED£½90،م£¬،دADC£½،دBDE£¬
،à،دCAD£½،دCBH£¬
،كAC£½BC£¬،دACD£½،دBCH£½90،م£¬
،à،÷ACD،ص،÷BCH£¨ASA£©£¬
،àAD£½BH£½2BE£»
£¨3£©OC£½BF+OA£¬
ہيسةتا£؛بçح¼¢غ£¬¹C×÷CM،حBF£¬½»FBµؤرس³¤دكسعM£¬

ح¬ہي؟ةµأ£؛،÷AOC،ص،÷BMC£¨AAS£©£¬
،àAO£½BM£¬OC£½CM£¬
،ك،دCOF£½،دOFM£½،دM£½90،م£¬
،àثؤ±كذخOCMFخھ¾طذخ£¬
،àFM£½OC£¬
،àFM£½BF+BM£¬
،àOC£½BF+OA£®

 ¾ظز»·´بح¬²½اة½²¾«ء·دµءذ´ً°¸
¾ظز»·´بح¬²½اة½²¾«ء·دµءذ´ً°¸ ؟عثمسëس¦سأجâ؟¨دµءذ´ً°¸
؟عثمسëس¦سأجâ؟¨دµءذ´ً°¸ أûت¦µم¾¦×ض´ت¾ن¶خئھدµءذ´ً°¸
أûت¦µم¾¦×ض´ت¾ن¶خئھدµءذ´ً°¸،¾جâؤ؟،؟×ماٍشث¶¯ش±½«×ماٍرطسëµطأو³ةز»¶¨½ا¶بµؤ·½دٍجك³ِ£¬×ماٍ·ةذذµؤآ·دكتاز»جُإ×خïدك£¬²»؟¼آا؟صئّ×èء¦£¬×ماٍ¾àہëµطأوµؤ¸ك¶ب![]() £¨µ¥خ»£؛
£¨µ¥خ»£؛![]() £©سë×ماٍ±»جك³ِ؛َ¾¹µؤت±¼ن
£©سë×ماٍ±»جك³ِ؛َ¾¹µؤت±¼ن![]() £¨µ¥خ»£؛
£¨µ¥خ»£؛![]() £©ض®¼نµؤ¹طدµبçدآ±ي£؛
£©ض®¼نµؤ¹طدµبçدآ±ي£؛
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ، |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | ، |
دآءذ½لآغ£؛¢ظ×ماٍ¾àہëµطأوµؤ×î´َ¸ك¶بخھ![]() £»¢ع×ماٍ·ةذذآ·دكµؤ¶ش³ئضلتاض±دك
£»¢ع×ماٍ·ةذذآ·دكµؤ¶ش³ئضلتاض±دك![]() £»¢غ×ماٍ±»جك³ِ
£»¢غ×ماٍ±»جك³ِ![]() ت±آنµط£»¢ـ×ماٍ±»جك³ِ
ت±آنµط£»¢ـ×ماٍ±»جك³ِ![]() ت±£¬¾àہëµطأوµؤ¸ك¶بتا
ت±£¬¾àہëµطأوµؤ¸ك¶بتا![]() .
.
ئنضذصب·½لآغµؤ¸ِتتا£¨ £©
A£®1 B£®2 C£®3 D£®4




