题目内容
【题目】如图，梯形ABCD中，
，且AD：
：3，对角线AC，BD交于点O，那么
：
：
______．
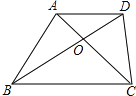
【答案】1：9：3
【解析】
先根据AD∥BC,可判定△AOD∽△COB, 由于AD：BC=1：3,可得OD：OB=AD：BC=1：3,根据等高的两个三角形,两个三角形的面积比等于对应的底边之比,可得S△AOD：S△AOB=1：3,再根据相似三角形的面积比等于相似比的平方倍可得S△AOD：S△BOC=1：9.
∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD：BC=1：3,
∴OD：OB=AD：BC=1：3,
∴S△AOD：S△AOB=1：3,
∴S△AOD：S△BOC=1：9,
∴S△AOD：S△BOC：S△AOB =1：9：3,
故答案为:1:9:3.
练习册系列答案
相关题目
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x＋40 | 90 |
每天销量（件） | 200－2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元[
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.
