题目内容
【题目】己知:![]() 为等边三角形,点E为射线AC上一点,点D为射线CB上一点,
为等边三角形,点E为射线AC上一点,点D为射线CB上一点,![]() .
.
(1)如图1,当E在AC的延长线上且![]() 时,AD是
时,AD是![]() 的中线吗?请说明理由;
的中线吗?请说明理由;
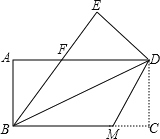
(2)如图2,当E在AC的延长线上时,![]() 等于AE吗?请说明理由;
等于AE吗?请说明理由;
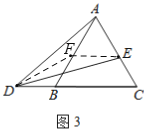
(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE的数量关系.

【答案】(1)是,理由见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)由等边三角形的性质得∠BAC=∠ACD=60°,由等腰三角形的性质得∠CDE=∠E,再根据三角形外角的性质可得∠E=30°,继而可得 ∠DAC=∠E=30°,得出AD平分∠BAC,由此即可得AD是△ABC的中线;
(2)在AB上取BH=BD,连接DH,利用AHD≌△DCE得出DH=CE,得出AE=AB+BD,
(3)在AB上取AF=AE,连接DF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB-BD=AE.
(1)是,理由如下:
∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,
∵CE=CD,
∴∠CDE=∠E,
∵∠ACD=∠E+∠CDE,
∴∠E=30°,
∵AD=DE,
∴∠DAC=∠E=30°,
∴∠DAC=![]() ∠BAC,
∠BAC,
即AD平分∠BAC,
∴AD是△ABC的中线;
(2)![]() ,理由如下:
,理由如下:
如图2,在AB上取BH=BD,连接DH,
∵△ABC是等边三角形,
∴∠BAC=∠ACD=∠B=60°,AB=AC,
∴∠DCE=120°,△BDH是等边三角形,
∴DH=BD,∠DHB=60°,
∴∠AHD=120°,∠DHB=∠CAB,
∴∠DCE=∠AHD,DH//AC,
∵AD=DE,
∴∠E=∠DAC,
∵DH//AC,
∴∠HAD=∠DAC,
∴∠HAD=∠E,
∴△ADH≌△DEC,
∴DH=CE,
∴CE=BD,
∴AB+BD=AC+CE=AE;

(3)AE=AB-BD,理由如下:
如图3,在AB上取AF=AE,连接DF,EF,
∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴△AEF是等边三角形,
∴AF=EF,∠AFE=∠AFE=∠FAE=60°,
∴∠AFE=∠ABC,
∴EF//BC,
∴∠FED=∠EDB,
∵AD=DE,DF=DF,AF=EF,
∴△ADF≌△EDF,
∴∠DAF=∠DEF,∠ADF=∠EDF,
∵∠DFB=∠DAF+∠ADF,∠FDB=∠EDF+EDB,
∴∠DFB=∠FDB,
∴BD=BF,
∵AB-BF=AF,
∴AB-BD=AE.