��Ŀ����
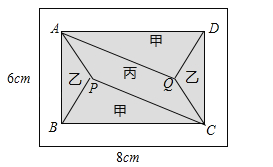
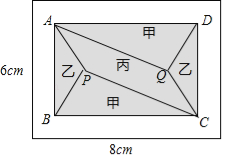
����Ŀ����2017�㽭ʡ�����У�С��������8m����6m�ij����ο��������ש���ֽ��仮�ֳ�һ��������ABCD�������Ӱ���֣���һ����������հײ��֣�������������üס��ҡ������ִ�ש���裬������PQ��AD����ͼ��ʾ��
��1�������������ִ�ש����Ϊ300Ԫ/m2�����ΪS��m2���������Ĵ�ש����Ϊ200Ԫ/m2����������Ĵ�ש�ܼ�Ϊ������12000Ԫ����S�����ֵ��
��2�������������BC=2��3����������ܿ�����ȣ�
����AB��BC�ij���
�����ס�������ש����֮��Ϊ300Ԫ/m2���ҡ�����ש����֮��Ϊ5��3�������������ִ�ש�ܼ�Ϊ4800Ԫ�������ש���۵�ȡֵ��Χ��
���𰸡���1��24����2����AB=4��CB=6���ڱ���ש����3x�ķ�ΧΪ150��3x��300Ԫ/m2��
�����������⣨1����������ɵ�300S+��48��S��200��12000���ⲻ��ʽ���ɣ�
��2���������������ܿ���Ϊa���������⣨6��2a������8��2a��=2��3�����a=1���ɴ˼��ɽ�����⣻
�����ҡ�����ש���۷ֱ�Ϊ5xԪ/m2��3xԪ/m2����ĵ���Ϊ��300��3x��Ԫ/m2����PQ��AD���ɵü����=����ABCD�������һ��=12�����ҵ����Ϊs����������Ϊ��12��s����������12��300��3x��+5xs+3x��12��s��=4800�����s=![]() ����0��s��12���ɵ�0��
����0��s��12���ɵ�0��![]() ��12���ⲻ��ʽ����
��12���ⲻ��ʽ����
�����������1��������300S+��48��S��200��12000��
���S��24��
��S�����ֵΪ24��
��2���������������ܿ���Ϊa���������⣨6��2a������8��2a��=2��3�����a=1��
��AB=6��2a=4��CB=8��2a=6��
�����ҡ�����ש���۷ֱ�Ϊ5xԪ/m2��3xԪ/m2����ĵ���Ϊ��300��3x��Ԫ/m2��
��PQ��AD��
�������=����ABCD�������һ��=12�����ҵ����Ϊs����������Ϊ��12��s����
������12��300��3x��+5xs+3x��12��s��=4800��
���s=![]() ��
��
��0��s��12��
��0��![]() ��12��
��12��
��0��x��50��
������ש����3x�ķ�ΧΪ0��3x��150Ԫ/m2��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�