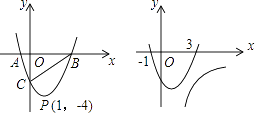题目内容
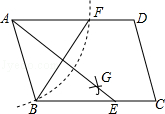
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.
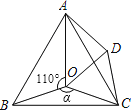
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
【答案】(1)△ADO是直角三角形;(2)当α为110°、125°、140°时,三角形AOD是等腰三角形.
【解析】
试题分析:(1)首先根据已知条件可以证明△BOC≌△ADC,然后利用全等三角形的性质可以求出∠ADO的度数,由此即可判定△AOD的形状;
(2)利用(1)和已知条件及等腰三角形的性质即可求解.
试题解析:(1)∵△OCD是等边三角形,
∴OC=CD,
而△ABC是等边三角形,
∴BC=AC,
∵∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC与△ADC中,
∵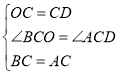 ,
,
∴△BOC≌△ADC,
∴∠BOC=∠ADC,
而∠BOC=α=150°,∠ODC=60°,
∴∠ADO=150°-60°=90°,
∴△ADO是直角三角形;
(2)∵设∠CBO=∠CAD=a,∠ABO=b,∠BAO=c,∠CAO=d,
则a+b=60°,b+c=180°-110°=70°,c+d=60°,a+d=50°∠DAO=50°,
∴b-d=10°,
∴(60°-a)-d=10°,
∴a+d=50°,
即∠CAO=50°,
①要使AO=AD,需∠AOD=∠ADO,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
∴190°-α=50°,
∴α=140°.
所以当α为110°、125°、140°时,三角形AOD是等腰三角形.

【题目】在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 3 | 1 |
(1)该小组射击数据的众数是 .
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
【题目】某课题组为了解全市八年级学生对数学知识的掌握情况,在一次数学检测中,从全市24000名八年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段 | 频数 | 频率 |
| 20 | 0.10 |
60≤ | 28 | 0.14 |
70≤ | 54 | 0.27 |
80≤ |
| 0.20 |
90≤ | 24 | 0.12 |
100≤ | 18 |
|
110≤ | 16 | 0.08 |
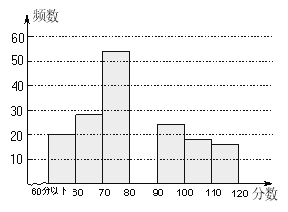
请根据以上图表提供的信息,解答下列问题:
(1)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() = ,
= ,![]() = ;
= ;
(2)请在图中,补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市24000名八年级考生数学成绩为优秀的学生约有多少名?