题目内容
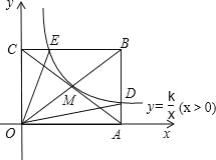
【题目】如图，已知一次函数
的图像与
轴交于点
，一次函数
的图像过点
，且与
轴及的图像分别交于点
、
，点坐标为
.
（1）求n的值及一次函数的解析式.
（2）求四边形
的面积.
【答案】(1) n =
；y=2x+4；(2）S=
【解析】
（1）根据点D在函数y=－x+2的图象上，即可求出n的值；再利用待定系数法求出k，b的值；
（2）用三角形OBC的面积减去三角形ABD的面积即可．
（1）∵点D（－
，n）在直线y=－x+2上，∴n=+2=．
∵一次函数经过点B（0，4）、点D（－
），∴
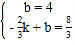，解得：
．故一次函数的解析式为：y=2x+4；
（2）直线y=2x+4与x轴交于点C，∴令y=0，得：2x+4=0，解得：x=－2，∴OC=2．
∵函数y=－x+2的图象与y轴交于点A，∴令x=0，得：y=2，∴OA=2．
∵B（0，4），∴OB=4，∴AB=2．
S△BOC=
×2×4=4，S△BAD=×2×=，∴S四边形AOCD=S△BOC﹣S△BAD=4﹣=．
练习册系列答案
相关题目
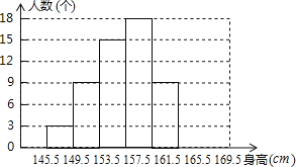
【题目】 为了解九年级女生的身高（单位：cm）情况，某中学对部分九年级女生身高进行了一次测量，所得数据整理后列出了频数分布表，并画了部分频数分布直方图（图、表如图）：
分组 | 频数 | 频率 |
145.5-149.5 | 3 | 0.05 |
149.5-153.5 | 9 | n |
153.5-157.5 | m | 0.25 |
157.5-161.5 | 18 | 0.30 |
161.5-165.5 | 9 | 0.15 |
165.5-169.5 | 6 | 0.10 |
合计 | M | N |
根据以上图表，回答问题．
（1）M=______，m=______，N=______，n=______；
（2）补全频数分布直方图；
（3）若九年级有600名学生，则身高在161.5-165.5范围约为多少人？
