题目内容
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
【答案】(Ⅰ)(7,﹣3);(Ⅱ)点P(﹣2,1)(Ⅲ)k=±2
【解析】
(Ⅰ)根据“k属派生点”计算可得;(Ⅱ)设点P的坐标为(x、y),根据“k属派生点”定义及P′的坐标列出关于x、y的方程组,解之可得;(Ⅲ)先得出点P′的坐标为(a,ka),由线段PP′的长度为线段OP长度的2倍列出方程,解之可得.
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为(﹣2+3×3,﹣2×3+3),即(7,﹣3),
故答案为:(7,﹣3);
(Ⅱ)设P(x,y),
依题意,得方程组:![]() ,
,
解得![]() ,
,
∴点P(﹣2,1).
(Ⅲ)∵点P(a,b)在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka),
∴线段PP′的长为点P′到x轴距离为|ka|,
∵P在x轴正半轴,线段OP的长为a,
根据题意,有|PP'|=2|OP|,
∴|ka|=2a,
∵a>0,
∴|k|=2.
从而k=±2.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
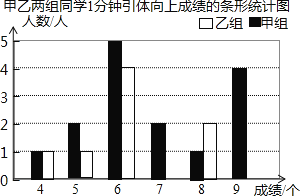
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.