题目内容
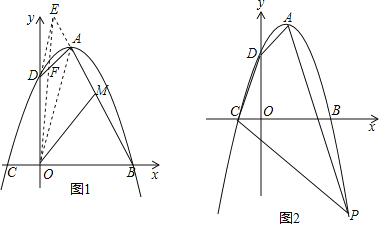
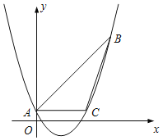
【题目】如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
(1)求这条抛物线的解析式.
(2)求tan∠ABC的值.
(3)若点D为抛物线的顶点,点E是直线AC上一点,当△CDE与△ABC相似时,求点E的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(4,1)或E(﹣3,1).
;(3)E(4,1)或E(﹣3,1).
【解析】
(1)将点A和点B的坐标代入抛物线的解析式求得a、c的值即可;
(2)过点B作BH⊥AC交AC延长线于点H,过点C作CG⊥AB于点G,先证明△ABH和△ACG均为等腰直角三角形,再求出CG和BG的长,然后依据锐角三角函数的定义求解即可;
(3)过点D作DK⊥AC,垂足为K,先证明△DCK为等腰直角三角形,则∠DCK=∠BAC,当![]() 或
或![]() 时,△CDE与△ABC相似,然后可求得CE的长.
时,△CDE与△ABC相似,然后可求得CE的长.
解:(1)∵抛物线y=ax2﹣2x+c经过点A(0,1)和点B(9,10),
∴![]() ,解得
,解得![]() .
.
∴这条抛物线的解析式为![]() .
.
(2)过点B作BH⊥AC交AC延长线于点H,
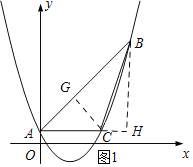
∵AC∥x轴,A(0,1),B(9,10),∴H(9,1),∴BH=AH=9.
又∵∠BHA=90°,∴△HAB是等腰直角三角形,∴∠HAB=45°.
∵AC∥x轴,A(0,1),对称轴为直线![]() ,∴C(6,1).
,∴C(6,1).
过点C作CG⊥AB,垂足为点G,
∵∠GAC=45°,∠AGC=90°,∴![]() ,∴
,∴![]() .
.
又∵在Rt△ABH中,![]() ,∴
,∴![]() .
.
∴在Rt△BCG中,![]() .
.
(3)如图2所示:过点D作DK⊥AC,垂足为K,

∵点D是抛物线![]() 的顶点,∴D(3,﹣2).
的顶点,∴D(3,﹣2).
∴K(3,1),∴CK=DK=3.
又∵∠CKD=90°,∴△CDK是等腰直角三角形,∴∠DCK=45°
又∵∠BAC=45°,
∴∠DCK=∠BAC.
∴要使△CDE与△ABC相似,则点E在点C的左侧.
当![]() 时,则
时,则![]() ,∴EC=2,∴E(4,1);
,∴EC=2,∴E(4,1);
当![]() 时,则
时,则![]() ,∴EC=9,∴E(﹣3,1).
,∴EC=9,∴E(﹣3,1).
综上所述,当△CDE与△ABC相似时,点E的坐标为(4,1)或(﹣3,1).

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案