Question

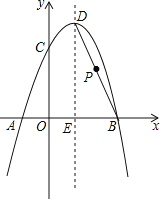
【题目】在平面直角坐标系xOy中，顶点为A的抛物线与x轴交于B、C两点，与y轴交于点D，已知A(1，4)，B(3，0)．

(1)求抛物线对应的二次函数表达式；

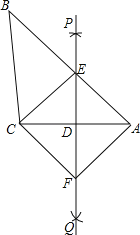
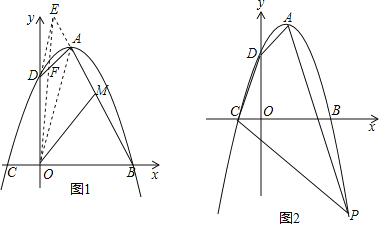
(2)探究：如图1，连接OA，作DE∥OA交BA的延长线于点E，连接OE交AD于点F，M是BE的中点，则OM是否将四边形OBAD分成面积相等的两部分？请说明理由；

(3)应用：如图2，P(m，n)是抛物线在第四象限的图象上的点，且m+n＝﹣1，连接PA、PC，在线段PC上确定一点M，使AN平分四边形ADCP的面积，求点N的坐标．提示：若点A、B的坐标分别为(x1，y1)、(x2，y2)，则线段AB的中点坐标为(，)．

Answer 1

【答案】(1)y＝﹣x2+2x﹣3；(2)OM将四边形OBAD分成面积相等的两部分，理由见解析；(3)点N(，﹣)．

【解析】

(1)函数表达式为：y＝a(x﹣1)2+4，将点B坐标的坐标代入上式，即可求解；

(2)利用同底等高的两个三角形的面积相等，即可求解；

(3)由(2)知：点N是PQ的中点，根据C,P点的坐标求出直线PC的解析式，同理求出AC,DQ的解析式，并联立方程求出Q点的坐标，从而即可求N点的坐标．

(1)函数表达式为：y＝a(x﹣1)2+4，

将点B坐标的坐标代入上式得：0＝a(3﹣1)2+4，

解得：a＝﹣1，

故抛物线的表达式为：y＝﹣x2+2x﹣3；

(2)OM将四边形OBAD分成面积相等的两部分，理由：

如图1，∵DE∥AO，S△ODA＝S△OEA，

S△ODA+S△AOM＝S△OEA+S△AOM，即：S四边形OMAD＝S△OBM，

∴S△OME＝S△OBM，

∴S四边形OMAD＝S△OBM；

(3)设点P(m，n)，n＝﹣m2+2m+3，而m+n＝﹣1，

解得：m＝﹣1或4，故点P(4，﹣5)；

如图2，故点D作QD∥AC交PC的延长线于点Q，

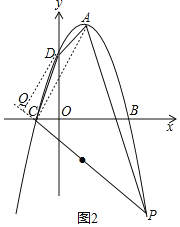
由(2)知：点N是PQ的中点，

设直线PC的解析式为y=kx+b，

将点C(﹣1，0)、P(4，﹣5)的坐标代入得：，

解得：，

所以直线PC的表达式为：y＝﹣x﹣1…①，

同理可得直线AC的表达式为：y＝2x+2，

直线DQ∥CA，且直线DQ经过点D(0，3)，

同理可得直线DQ的表达式为：y＝2x+3…②，

联立①②并解得：x＝﹣，即点Q(﹣，)，

∵点N是PQ的中点，

由中点公式得：点N(，﹣)．