题目内容
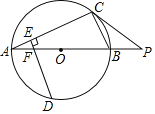
【题目】(新知探究)新定义:平面内两定点 A, B ,所有满足![]() k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
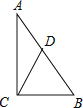
(问题解决)如图,在ABC 中,CB 4 , AB 2AC ,则ABC 面积的最大值为_____.
【答案】![]()
【解析】
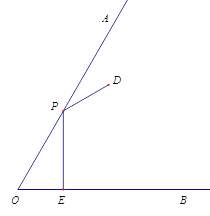
以A为顶点,AC为边,在△ABC外部作∠CAP=∠ABC,AP与BC的延长线交于点P,证出△APC∽△BPA,列出比例式可得BP=2AP,CP=![]() AP,从而求出AP、BP和CP,即可求出点A的运动轨迹,最后找出距离BC最远的A点的位置即可求出结论.
AP,从而求出AP、BP和CP,即可求出点A的运动轨迹,最后找出距离BC最远的A点的位置即可求出结论.
解:以A为顶点,AC为边,在△ABC外部作∠CAP=∠ABC,AP与BC的延长线交于点P,
∵∠APC=∠BPA, AB 2AC
∴△APC∽△BPA,
∴![]()
∴BP=2AP,CP=![]() AP
AP
∵BP-CP=BC=4
∴2AP-![]() AP=4
AP=4
解得:AP=![]()
∴BP=![]() ,CP=
,CP=![]() ,即点P为定点
,即点P为定点
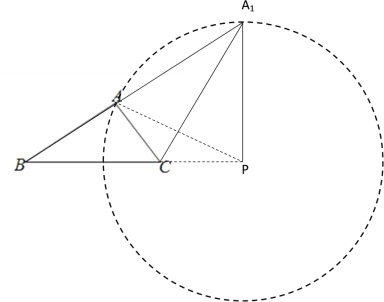
∴点A的轨迹为以点P为圆心,![]() 为半径的圆上,如下图所示,过点P作BC的垂线,交圆P于点A1,此时A1到BC的距离最大,即ABC的面积最大
为半径的圆上,如下图所示,过点P作BC的垂线,交圆P于点A1,此时A1到BC的距离最大,即ABC的面积最大
S△A1BC=![]() BC·A1P=
BC·A1P=![]() ×4×
×4×![]() =
=![]()
即ABC面积的最大值为![]()
故答案为:![]() .
.

练习册系列答案
相关题目