题目内容
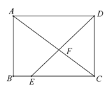
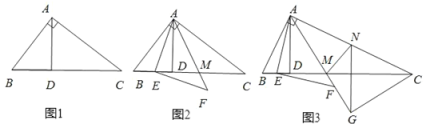
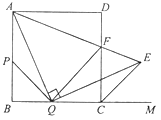
【题目】如图,在边长为2的正方形![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的两个动点(与点
上的两个动点(与点![]() 、
、![]() 、
、![]() 不重合),且始终保持
不重合),且始终保持![]() ,
,![]() ,
,![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,并求出此时
,并求出此时![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)当![]() 时,
时,![]() ;
;![]()
![]() .
.
【解析】
(1)判断出△PBQ是等腰直角三角形,然后求出∠APQ=∠QCE=135°,再根据同角的余角相等求出∠PAQ=∠CQE,再求出AP=CQ,然后利用“角边角”证明即可;
(2)根据全等三角形对应边相等可得AQ=EQ,判断出△AQE是等腰直角三角形,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,再证明
,再证明![]() ;
;
(3)连结![]() ,设
,设![]() ,推出
,推出![]() 是等腰直角三角形°,再证明
是等腰直角三角形°,再证明![]() ,根据全等三角形对应边相等可得QF=GF,
,根据全等三角形对应边相等可得QF=GF,![]() ,
,![]() ,分别用x表示出DF、CF、QF,然后列出方程求出x,再求出△AQF的面积.
,分别用x表示出DF、CF、QF,然后列出方程求出x,再求出△AQF的面积.
(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴![]() ,
,
∴![]()
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() .
.
∴![]() .
.
∴![]() .
.
(2)由(1)知![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
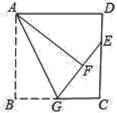
如图4,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,
,
其中点![]() 与点
与点![]() 重合,且点
重合,且点![]() 在直线
在直线![]() 上,
上,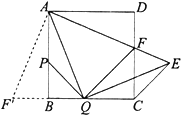
则![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
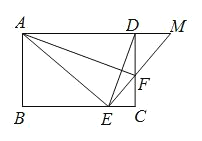
(3)连结![]() ,若
,若![]() ,
,
则![]() .
.
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,根据勾股定理,得
中,根据勾股定理,得![]() .
.
解这个方程,得![]() ,
, ![]() (舍去).
(舍去).
当![]() 时,
时,![]() .
.
此时,![]() ,∴
,∴![]() ,
,
∴![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目