Question

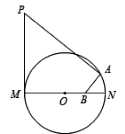
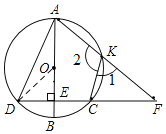
【题目】如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，点K为弧AC上的一个动点（K不与A，C重合），AK，DC延长线交于点F，连接CK．

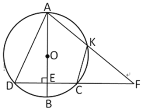
（1）求证：△ADF∽△CKF

（2）若AB=10，CD=6，求tan∠CKF的值

Answer 1

【答案】（1）见解析；（2）3

【解析】

（1）证明∠1=∠D，又∠F=∠F，可说明△ADF∽△CKF；
（2）连接OD，利用垂径定理即勾股定理求出OE长，则AE可知，在Rt△ADE中，tan∠ADE值可求，又∠CKF=∠ADE，所以tan∠CKF可求．

（1）∵四边形ADCK内接于⊙O，

∴∠D+∠2=180°．
∵∠1+∠2=180°，
∴∠1=∠D．
又∠F=∠F，
∴△ADF∽△CKF；
（2）连接OD，

∵AB=10，
∴AO=DO=5．
∵直径AB⊥CD，CD=6，
∴DE=CD=3．
在Rt△ODE中，利用勾股定理可得

，

∴AE=OA+OE=9．
在Rt△ADE中，，

∴，

∵∠CKF=∠ADE，
∴tan∠CKF=3．