ĢāÄæÄŚČŻ
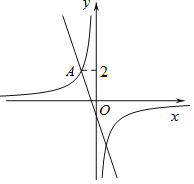
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ŅŃÖŖµć
ÖŠ£¬ŅŃÖŖµć![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬ŅŌ
ÖįÉĻ£¬ŅŌ![]() ĪŖÖ±¾¶×÷
ĪŖÖ±¾¶×÷![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬ĒŅŌŚµć
ÖįÉĻ£¬ĒŅŌŚµć![]() ÉĻ·½£¬¹żµć
ÉĻ·½£¬¹żµć![]() ×÷
×÷![]() µÄĒŠĻß
µÄĒŠĻß![]() £¬
£¬![]() ĪŖĒŠµć£¬Čē¹ūµć
ĪŖĒŠµć£¬Čē¹ūµć![]() ŌŚµŚŅ»ĻóĻŽ£¬Ōņ³Ę
ŌŚµŚŅ»ĻóĻŽ£¬Ōņ³Ę![]() ĪŖµć
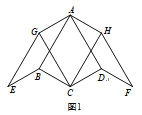
ĪŖµć![]() µÄĄėµć£®ĄżČē£¬Ķ¼1ÖŠµÄ
µÄĄėµć£®ĄżČē£¬Ķ¼1ÖŠµÄ![]() ĪŖµć
ĪŖµć![]() µÄŅ»øöĄėµć£®
µÄŅ»øöĄėµć£®
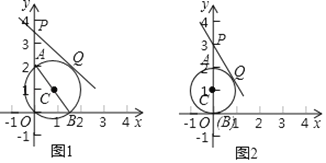
£Ø1£©ŅŃÖŖµć![]() £¬
£¬![]() ĪŖ
ĪŖ![]() µÄĄėµć£®
µÄĄėµć£®
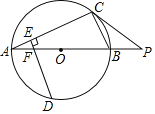
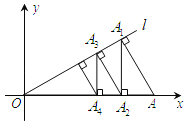
¢ŁČēĶ¼2£¬Čō![]() £¬ŌņŌ²ŠÄ
£¬ŌņŌ²ŠÄ![]() µÄ×ų±źĪŖ__________£¬Ļ߶Ī
µÄ×ų±źĪŖ__________£¬Ļ߶Ī![]() µÄ³¤ĪŖ__________£»
µÄ³¤ĪŖ__________£»
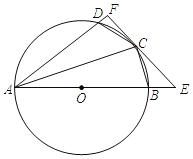
¢ŚČō![]() £¬ĒóĻ߶Ī
£¬ĒóĻ߶Ī![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ŅŃÖŖ![]() £¬Ö±Ļß
£¬Ö±Ļß![]() £®
£®
¢Łµ±![]() Ź±£¬ČōÖ±Ļß
Ź±£¬ČōÖ±Ļß![]() ÉĻ“ęŌŚ
ÉĻ“ęŌŚ![]() µÄĄėµć
µÄĄėµć![]() £¬Ōņµć
£¬Ōņµć![]() ׯ×ų±ź
ׯ×ų±ź![]() µÄ×ī“óÖµĪŖ__________£»
µÄ×ī“óÖµĪŖ__________£»
¢Ś¼ĒÖ±Ļß![]() ŌŚ
ŌŚ![]() µÄ²æ·ÖĪŖĶ¼ŠĪ
µÄ²æ·ÖĪŖĶ¼ŠĪ![]() £¬Čē¹ūĶ¼ŠĪ
£¬Čē¹ūĶ¼ŠĪ![]() ÉĻ“ęŌŚ
ÉĻ“ęŌŚ![]() µÄĄėµć£¬Ö±½ÓŠ“³ö
µÄĄėµć£¬Ö±½ÓŠ“³ö![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
”¾“š°ø”æ(1)¢Ł£Ø0£¬1£©£»![]() £»ĻźĒé¼ū½āĪö£»¢Ś
£»ĻźĒé¼ū½āĪö£»¢Ś![]() £¬ĻźĒé¼ū½āĪö£»£Ø2£©¢Ł6£¬ĻźĒé¼ū½āĪö£»¢Śµ±k£¼0Ź±£¬1-2
£¬ĻźĒé¼ū½āĪö£»£Ø2£©¢Ł6£¬ĻźĒé¼ū½āĪö£»¢Śµ±k£¼0Ź±£¬1-2![]() <k”Ü
<k”Ü![]() »ņµ±k£¾0Ź±£¬
»ņµ±k£¾0Ź±£¬![]() ”Ük<1+2
”Ük<1+2![]() £»ĻźĒé¼ū½āĪö£»
£»ĻźĒé¼ū½āĪö£»
”¾½āĪö”æ
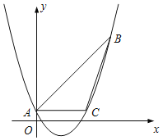
£Ø1£©¢ŁČēĶ¼æÉÖŖ£ŗC(0£¬1)£¬ŌŚRt![]() PQCÖŠ£¬CQ=1£¬PC=2£¬æɵĆĻ߶Ī
PQCÖŠ£¬CQ=1£¬PC=2£¬æɵĆĻ߶Ī![]() µÄ³¤£»
µÄ³¤£»
¢ŚČēĶ¼£¬¹żC×÷CM”ĶyÖįÓŚµćM£¬Į¬½ÓCP£¬CQ£¬M(0£¬1)£¬ŌŚRt![]() ACMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆCA=
ACMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆCA=![]() £¬CQ=
£¬CQ=![]() £¬ŌŚRt
£¬ŌŚRt![]() PCMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPC=
PCMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPC=![]() £¬ŌŚRt
£¬ŌŚRt![]() PCQÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPQ=
PCQÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPQ=![]() £»
£»
£Ø2£©¢Łµ±k=1Ź±£¬y=x+4£¬Q£Øt-4£¬t£©£¬PµÄׯ×ų±źĪŖ4Ź±£¬PQÓėŌ²CĻąĒŠ£¬ÉčB£Øm£¬0£©£¬ŌņŌ²ŠÄĪŖ![]() £¬ÓÉCQ”ĶPQ£¬æÉĒóCQµÄ½āĪöŹ½ĪŖ
£¬ÓÉCQ”ĶPQ£¬æÉĒóCQµÄ½āĪöŹ½ĪŖ![]() £¬Qµćŗį×ų±źĪŖ
£¬Qµćŗį×ų±źĪŖ![]() £¬ŌņC£Ø2t-5£¬1£©£¬ŌŁÓÉCQ=AC£¬µĆµ½t=6»ņt=2£»
£¬ŌņC£Ø2t-5£¬1£©£¬ŌŁÓÉCQ=AC£¬µĆµ½t=6»ņt=2£»
¢Śy=kx+k+3¾¹ż¶Øµć£Ø-1£¬3)£¬PQŹĒŌ²µÄĒŠĻߣ¬AOŹĒŌ²µÄĻŅ£¬ŌņÓŠ![]() £¬µ±k<0Ź±£¬QµćµÄŌŚ¶Ėµć£Ø-1£¬3£©ŗĶ£Ø1£¬2k+3£©Ö®¼äŌĖ¶Æ£¬µ±P£Ø0£¬4£©Ź±£¬PQ=2
£¬µ±k<0Ź±£¬QµćµÄŌŚ¶Ėµć£Ø-1£¬3£©ŗĶ£Ø1£¬2k+3£©Ö®¼äŌĖ¶Æ£¬µ±P£Ø0£¬4£©Ź±£¬PQ=2![]() £¬.ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4-2
£¬.ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4-2![]() £©£¬“ĖŹ±k=1-2
£©£¬“ĖŹ±k=1-2![]() £¬µ±P£Ø0£¬3£©Ź±£¬PQ=
£¬µ±P£Ø0£¬3£©Ź±£¬PQ=![]() £¬Q£Ø1£¬2k+3£©£¬
£¬Q£Ø1£¬2k+3£©£¬![]() £¬ĖłŅŌ1-2
£¬ĖłŅŌ1-2![]() <k”Ü
<k”Ü![]() £»µ±k>0Ź±£¬µ±P£Ø0£¬4)Ź±£¬PQ=2
£»µ±k>0Ź±£¬µ±P£Ø0£¬4)Ź±£¬PQ=2![]() £¬ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4+2
£¬ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4+2![]() £©£¬“ĖŹ±k=1+2
£©£¬“ĖŹ±k=1+2![]() £¬µ±P(0£¬3)Ź±£¬PQ=
£¬µ±P(0£¬3)Ź±£¬PQ=![]() £¬Q£Ø1£¬2k+3£©£¬
£¬Q£Ø1£¬2k+3£©£¬![]() £¬
£¬![]() ”Ük<1+2
”Ük<1+2![]() £»
£»
½ā£ŗ
£Ø1£©¢ŁČēĶ¼æÉÖŖ£ŗC£Ø0£¬1£©£¬
ŌŚRt![]() PQCÖŠ£¬CQ=1£¬PC=2£¬
PQCÖŠ£¬CQ=1£¬PC=2£¬
”ą![]() £»
£»
¹Ź“š°øĪŖ£ŗ£Ø0£¬1£©£»![]() £»
£»
¢ŚČēĶ¼£¬¹żC×÷CM”ĶyÖįÓŚµćM£¬Į¬½ÓCP£¬CQ£¬
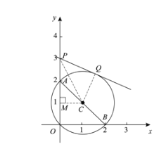
”ßA£Ø0£¬2£©£¬B£Ø2£¬0£©£¬
”ąC£Ø1£¬1£©£¬
”ąM£Ø0£¬1£©£¬
ŌŚRt![]() ACMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆCA=
ACMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆCA=![]() £¬
£¬
”ąCQ=![]() £¬
£¬
”ßP£Ø0£¬3£©£¬M£Ø0£¬1£©£¬
”ąPM=2£¬
ŌŚRt![]() PCMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPC=
PCMÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPC=![]() £¬
£¬
ŌŚRt![]() PCQÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPQ=
PCQÖŠ£¬Óɹ“¹É¶ØĄķæɵĆPQ=![]() £»
£»
£Ø2£©¢Łµ±k=1Ź±£¬y=x+4£¬
”ąQ£Øt-4£¬t£©£¬
”ß![]() £¬
£¬
”ąPµÄׯ×ų±źĪŖ4Ź±£¬PQÓėŌ²CĻąĒŠ£¬
ÉčB£Øm£¬0£©£¬
”ąC![]() £¬
£¬
”ßCQ”ĶPQ£¬
”ąCQµÄ½āĪöŹ½ĪŖ![]() £¬
£¬
”ąQµćŗį×ų±źĪŖ![]() £¬
£¬
”ą![]() £¬
£¬
”ąm=4t-10£¬
”ąC£Ø2t-5£¬1£©£¬
”ßCQ=AC£¬
”ą![]() £¬
£¬
”ąt=6»ņt=2£»
”ątµÄ×ī“óÖµĪŖ6£»
¹Ź“š°øĪŖ£ŗ6.
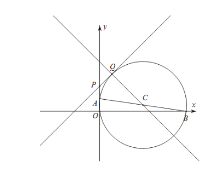
¢Ś”ß-1”Üx”Ü1£¬
”ßy=kx+k+3¾¹ż¶Øµć£Ø-1£¬3)£¬
”ßPQŹĒŌ²µÄĒŠĻߣ¬AOŹĒŌ²µÄĻŅ£¬
”ą![]() £¬
£¬
µ±k<0Ź±£¬QµćµÄŌŚ¶Ėµć£Ø-1£¬3£©ŗĶ£Ø1£¬2k+3£©Ö®¼äŌĖ¶Æ£¬
µ±P£Ø0£¬4£©Ź±£¬PQ=2![]() £¬
£¬
.ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4-2![]() £©£¬
£©£¬
“ĖŹ±k=1-2![]() £¬
£¬
µ±P£Ø0£¬3£©Ź±£¬PQ=![]() £¬Q£Ø1£¬2k+3£©£¬
£¬Q£Ø1£¬2k+3£©£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
¼“1-2![]() <k”Ü
<k”Ü![]() £»
£»
µ±k>0Ź±£¬µ±P£Ø0£¬4)Ź±£¬PQ=2![]() £¬
£¬
ŅŌPĪŖŌ²ŠÄ£¬PQ³¤ĪŖ°ė¾¶µÄŌ²ÓėyÖį½»ÓŚµć£Ø0£¬4+2![]() £©£¬
£©£¬
“ĖŹ±k=1+2![]() £¬
£¬
µ±P(0£¬3)Ź±£¬PQ=![]() £¬
£¬
Q£Ø1£¬2k+3£©£¬
![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
¼“![]() ”Ük<1+2
”Ük<1+2![]() £»
£»

 ĘŚÄ©ø“Ļ°¼ģ²āĻµĮŠ“š°ø
ĘŚÄ©ø“Ļ°¼ģ²āĻµĮŠ“š°ø ³¬ÄÜѧµäµ„ŌŖĘŚÖŠĘŚÄ©×ØĢā³å“Ģ100·ÖĻµĮŠ“š°ø
³¬ÄÜѧµäµ„ŌŖĘŚÖŠĘŚÄ©×ØĢā³å“Ģ100·ÖĻµĮŠ“š°ø »ĘøŌ360¶Č¶ØÖĘĆܾķĻµĮŠ“š°ø
»ĘøŌ360¶Č¶ØÖĘĆܾķĻµĮŠ“š°ø Ńō¹āæ¼³”µ„ŌŖ²āŹŌ¾ķĻµĮŠ“š°ø
Ńō¹āæ¼³”µ„ŌŖ²āŹŌ¾ķĻµĮŠ“š°ø