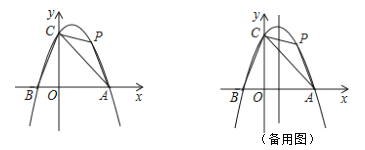题目内容
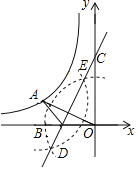
【题目】如图,已知![]() ,
,![]() 为反比例函数
为反比例函数![]() 的图象上一点,以
的图象上一点,以![]() 为直径的圆的圆心
为直径的圆的圆心![]() 在
在![]() 轴上,
轴上,![]() 与
与![]() 轴正半轴交于
轴正半轴交于![]() ,则
,则![]() 的值为( )
的值为( )
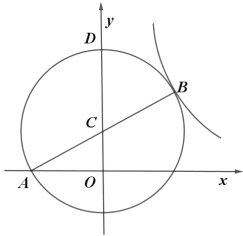
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过B点作BH⊥x轴于H点,由AB为直径,推出H在圆上,再由垂径定理求出OH的长,再在△COH中由勾股定理求出圆的半径,进而求出CO,最后再求出BH,求得![]() 的值.
的值.
解:过B点作BH⊥x轴于H点,连接CH,如下图所示:
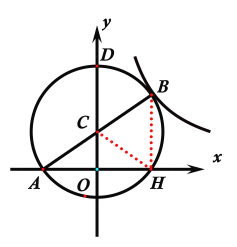
∵AB为圆的直径,且∠AHB=90°
由直径所对的圆周角为90°知:
H必在圆C上.
又AH⊥y轴,由垂径定理知:OA=OH=2.
设圆的半径CD=CH=r,则CO=DO-CD=4-r
在Rt△COH中,由勾股定理有:![]()
∴![]() ,解得
,解得![]()
∴CO =![]() =
=![]()
又O为AH的中点
∴CO为△ABH的中位线
∴BH=2CO=3
∴B点坐标为(2,3),故![]() =6.
=6.
故答案为:C.

练习册系列答案
相关题目
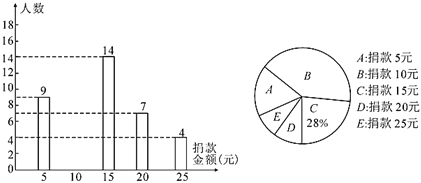
【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
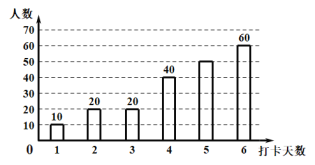
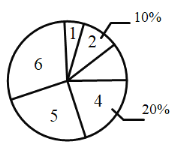
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?