题目内容
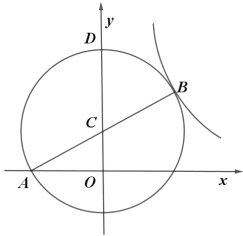
【题目】如图,点A在双曲线y=![]() (k<0)上,连接OA,分别以点O和点A为圆心,大于
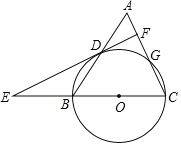
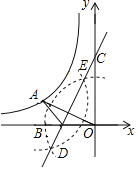
(k<0)上,连接OA,分别以点O和点A为圆心,大于![]() OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
【答案】﹣![]() .
.
【解析】
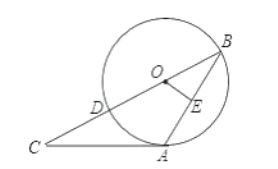
BC交OA于H,如图,利用基本作图得到CB垂直平分OA,则BO=BA=1,AH=OH,在Rt△OCB中先利用勾股定理计算出CB,再利用面积法计算出OH=![]() ,则OA=
,则OA=![]() ,设A(m,n),根据两点间的距离公式得到(m+1)2+n2=12,m2+n2=(
,设A(m,n),根据两点间的距离公式得到(m+1)2+n2=12,m2+n2=(![]() )2,解关于m、n的方程组得到A
)2,解关于m、n的方程组得到A![]() ,然后利用反比例函数图像上点的坐标特征求k的值.
,然后利用反比例函数图像上点的坐标特征求k的值.
BC交OA于H,如图,
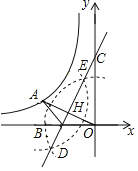
由作法得CB垂直平分OA,
∴BO=BA=1,AH=OH,∠OBH=90°,
∴B(﹣1,0),
在Rt△OCB中,
∵C(0,3),
∴OC=3,
∴CB=![]() =
=![]() ,
,
∵![]() ×OH×BC=
×OH×BC=![]() ×OB×OC,
×OB×OC,
∴OH=![]() ,
,
∴OA=2OH=![]() ,
,
设A(m,n),则(m+1)2+n2=12,m2+n2=(![]() )2,
)2,
解得m=![]() ,n=
,n=![]() ,
,
∴A ![]() ,
,
把A![]() 代入
代入![]() 得k=
得k=![]() .
.
故答案为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目