题目内容
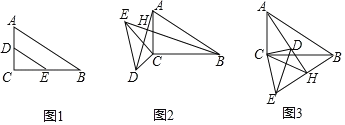
【题目】已知:已知Rt△ABC中,∠ACB=90°,D、E分别是AC、BC上的点,连DE,且![]() ,tanB
,tanB![]() ,如图1.
,如图1.
(1)如图2,将△CDE绕C点旋转,连AD、BE交于H,求证:AD⊥BE;
(2)如图3,当△CDE绕C点旋转过程中,当CH![]() 时,求
时,求![]() AH﹣BH的值;
AH﹣BH的值;
(3)若CD=1,当△CDE绕C点旋转过程中,直接写出AH的最大值是 .
【答案】(1)证明见解析;(2)![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)设BE交AC于O,首先证明△ACD∽△BCE,然后有∠DAC=∠EBC,通过等量代换即可得出结论;
(2)在HB上取一点T,使得HT![]() AH,连接AT,首先通过三角函数证明∠ATH=∠ABC,然后证明△AHT∽△ACB,进而可证△CAH∽△BAT,则有
AH,连接AT,首先通过三角函数证明∠ATH=∠ABC,然后证明△AHT∽△ACB,进而可证△CAH∽△BAT,则有![]() ,即可求解;
,即可求解;
(3)因为AH=ABsin∠ABH,所以当∠ABH最大时,AH的值最大,此时CE⊥BE,此时四边形ECDH是矩形,然后利用矩形的性质和勾股定理即可求解.
(1)如图2中,设BE交AC于O.

∵∠ACB=∠DCE=90°,
∴∠ACD=∠ECB.
∵![]() ,
,
∴![]() ,
,
∴△ACD∽△BCE,
∴∠DAC=∠EBC.
∵∠AOH=∠BOC,
∴∠AHO=∠BCO=90°,
∴AD⊥BE.
(2)如图2中,在HB上取一点T,使得HT![]() AH,连接AT.
AH,连接AT.
在Rt△AHT中,tan∠ATH![]() ,
,
∵tan∠ABC![]() ,
,
∴∠ATH=∠ABC.
∵∠ATH+∠HAT=90°,∠ABC+∠CAB=90°,
∴∠HAT=∠CAB,
∴∠CAH=∠BAT,
∴△AHT∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴△CAH∽△BAT,
∴![]() ,
,
∵HT![]() AH,
AH,
设AH=m,则HT![]() m,AT
m,AT![]() m,
m,
∴![]() ,
,
∴BT![]() .
.
(3)如图3中,

在Rt△AHB中,∵AH=ABsin∠ABH,∴当∠ABH最大时,AH的值最大,此时CE⊥BE.
∵∠DCE=∠CEH=∠EHD=90°,
∴此时四边形ECDH是矩形,
∴DH=EC,∠ADC=∠CDH=90°,
由题意CD=1,EC![]() ,AC
,AC![]() ,
,
∴DH=CE![]()
在Rt△ACD中,AD![]() ,
,
∴AH=AD+DH![]() 2
2![]() ,
,
∴AH的最大值为2![]() .
.

 名题金卷系列答案
名题金卷系列答案【题目】某商场举办的购物狂欢节期间与一知名APP支付平台合作,为答谢顾客,该商场对某款价格为a元/件(a>0)的商品开展促销活动.据统计,在此期间顾客购买该商品的支付情况如表:
支付方式 | 现金支付 | 购物卡支付 | APP支付 |
频率 | 10% | 30% | 60% |
优惠方式 | 按9折支付 | 按8折支付 | 其中有 |
将上述频率作为事件发生的概率,回答下列问题:
(1)顾客购买该商品使用APP支付的概率是 ;
(2)求顾客购买该商品获得的优惠超过20%的概率;
(3)该商品在促销优惠期间平均每件商品优惠多少元.
【题目】为推动实施健康中国战略,树立国家健康形象.手机APP推出多款健康运动软件,如“微信运动”.王老师随机调查了我校50名教师某日“微信运动”中的步数,并进行统计整理,绘制了如下的统计图表.
步数 | 频数 | 频率 |
| 8 |
|
| 15 | 0.3 |
|
| 0.24 |
| 10 | 0.2 |
| 3 | 0.06 |
| 2 | 0.04 |
合计 | 50 |
|
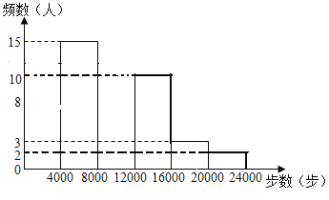
请根据以上信息,解答下列问题:
(1)![]() _______,
_______,![]() _______,
_______,![]() ________;
________;
(2)补全频数分布直方图;
(3)若某人一天的走路步数不低于16000步,将被“微信运动”评为“运动达人”.我市市区约有4000名初中教师,根据此项调查请估计市区被评为“运动达人”教师有多少名?