题目内容
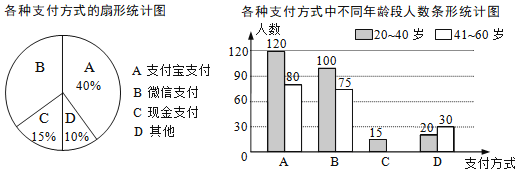
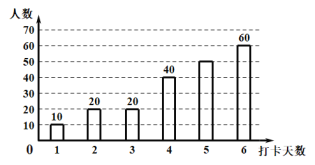
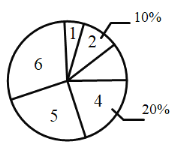
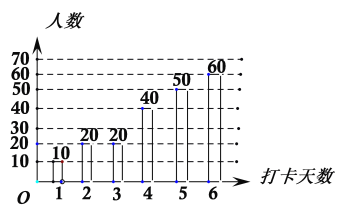
【题目】疫情期间，附中初
级老师们为了解孩子们在家每周体育锻炼打卡情况，收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图：
通过分析上面
个统计图，制作如下表格：
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
（1）填空：
_______，
_______，并补全条形统计图．
（2）因为疫情期间，在家体育锻炼条件受限，所以规定坚持打卡不低于
天即为合格．初级共有学生
人，请你估计初级学生中体育锻炼合格的人数．
（3）若统计时漏掉
名学生，先将他的打卡天数和原统计的打卡天数合并成一组新数据后，发现平均数增大了，则漏掉的这名学生坚持打卡天数最少是多少天？
【答案】(1) 
，
，补全图形如下所示；(2) 900人；(3) 5天.
【解析】
(1)通过扇形统计图中打卡天数为4天时所占的比例为20%，求出总人数，然后再减去打卡天数分别为1/2/3/4/6天的人数，即得到打卡天数为5天的人；然后再按打卡天数从小到大排列，最中间的打卡天数得出中位数a的值，出现次数最多的即为众数，求出b的值.
(2)算出打卡天数大于等于4天的人数的占比，然后再用1200乘以这个占比，即得到体育锻炼合格的人数.
(3)设漏掉的这名学生坚持打卡天数最少是x天，然后将新的平均数用x的代数式表示，其大于4.4天，进而得到不等式，求出x的最少天数.
解：(1)由题意，设打卡天数为4天的占20%，
故总人数为：40÷20%=200人
∴打卡天数为5天的人为：200-10-20-20-40-60=50人
故补全条形统计图如下所示：
总共200人，按从小到大排列最中间的两位数为100和101，第100和101名同学对应的打卡天数均是5天，故中位数是5，∴
众数是出现次数最多的数，∴
故答案为：，.
(2) 打卡天数大于等于4天的人数有：40+50+60=150人
其占200人的比重为：150÷200×100%=75%
故
人中体育锻炼合格的人数为：1200×75%=900人
故答案为：900人体育锻炼合格.
(3) 设漏掉的这名学生坚持打卡天数最少是x天，将漏掉的学生加入后，
新的打卡天数的平均数大于4，故由：
解不等式得：
又锻炼天数x为整数，∴
故答案为：这名学生坚持打卡天数最少是5天.
