题目内容
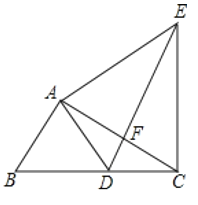
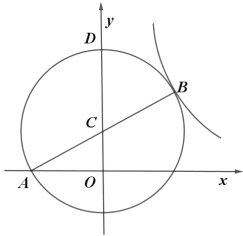
【题目】如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是_____.

【答案】![]() .
.
【解析】
如下图,过点B作BF⊥AC,过点E作EH⊥AC,由勾股定理可求AC=5,由面积法可求BF=![]() ,由勾股定理可求AF=
,由勾股定理可求AF=![]() ,由旋转的性质可得AB=BA',∠BAD=∠BA'D'=90°,可求AA'=
,由旋转的性质可得AB=BA',∠BAD=∠BA'D'=90°,可求AA'=![]() ,由等腰三角形的性质可求HC的长,通过证明△EHC∽△ABC,可得
,由等腰三角形的性质可求HC的长,通过证明△EHC∽△ABC,可得![]() ,可求EC的长,即可求解.
,可求EC的长,即可求解.
如下图,过点B作BF⊥AC,过点E作EH⊥AC,
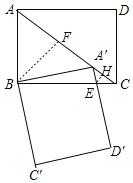
∵AB=3,AD=4,∠ABC=90°,
∴AC=![]() =5,
=5,
∵S△ABC=![]() AB×BC=
AB×BC=![]() AC×BF,
AC×BF,
∴3×4=5BF,
∴BF=![]()
∴AF=![]() ,
,
∵将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',
∴AB=BA',∠BAD=∠BA'D'=90°,且BF⊥AC,
∴∠BAC=∠BA'A,AF=A'F=![]() ,∠BA'A+∠EA'C=90°,
,∠BA'A+∠EA'C=90°,
∴A'C=AC﹣AA'=![]() ,
,
∵∠BA'A+∠EA'C=90°,∠BAA'+∠ACB=90°,
∴∠ACB=∠EA'C,
∴A'E=EC,且EH⊥AC,
∴A'H=HC=![]() A'C=
A'C=![]() ,
,
∵∠ACB=∠ECH,∠ABC=∠EHC=90°,
∴△EHC∽△ABC,
∴![]()
∴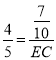
∴EC=![]() ,
,
∴BE=BC﹣EC=4﹣![]() =
=![]() ,
,
故答案为:![]() .
.

【题目】某商场举办的购物狂欢节期间与一知名APP支付平台合作,为答谢顾客,该商场对某款价格为a元/件(a>0)的商品开展促销活动.据统计,在此期间顾客购买该商品的支付情况如表:
支付方式 | 现金支付 | 购物卡支付 | APP支付 |
频率 | 10% | 30% | 60% |
优惠方式 | 按9折支付 | 按8折支付 | 其中有 |
将上述频率作为事件发生的概率,回答下列问题:
(1)顾客购买该商品使用APP支付的概率是 ;
(2)求顾客购买该商品获得的优惠超过20%的概率;
(3)该商品在促销优惠期间平均每件商品优惠多少元.
【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
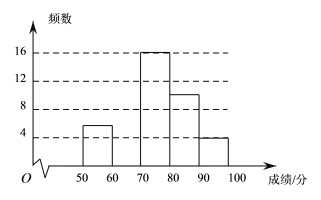
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 |
| 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | 4 | 0.08 |
(1)频数分布表中的![]() ;
;
(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.