题目内容
【题目】如图,在平面直角坐标中,二次函数y=ax2+bx+c的图象经过点A(6,0),B(﹣2,0),C(0,4).
(1)求二次函数y=ax2+bx+c的表达式;
(2)点P在第一象限的抛物线上,且能够使△ACP得面积最大,求点P的坐标;
(3)在(2)的前提下,在抛物线的对称轴上是否存在点Q,使得△APQ为直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
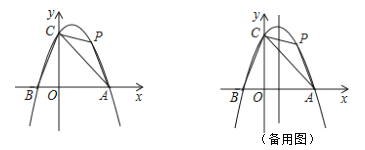
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)P(3,5);(3)点Q坐标为(2,﹣
x+4;(2)P(3,5);(3)点Q坐标为(2,﹣![]() )或(2,
)或(2,![]() )或(2,1)或(2,4)
)或(2,1)或(2,4)
【解析】
(1)将A、B、C三点代入,可求得抛物线的解析式;
(2)设P(m,﹣![]() m2+
m2+![]() m+4),先求出AC的解析式,从而得出点E的坐标,进而得出PE的长,从而求得用m表示的△PCA的面积,最后根据二次函数的特点,求出最值;
m+4),先求出AC的解析式,从而得出点E的坐标,进而得出PE的长,从而求得用m表示的△PCA的面积,最后根据二次函数的特点,求出最值;
(3)设设点Q的坐标为(2,m),根据平面直角坐标系中任意两点之间的距离公式求出AQ2、PQ2和AP2,存在3种情况,一种是∠QAP=90°,第二种是∠AQP=90°,第三种是∠QPA=90°时,利用勾股定理分别求解即可.
解:(1)把A(6,0),B(﹣2,0),C(0,4)的坐标代入y=ax2+bx+c,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4.
x+4.
(2)作PE∥OC交AC于E.
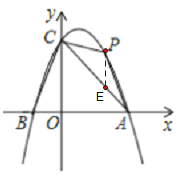
设P(m,﹣![]() m2+
m2+![]() m+4).
m+4).
设直线AC的解析式为y=kx+d
将点A和点C的坐标代入,得
![]()
解得: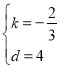
∴直线AC的解析式为y=﹣![]() x+4,
x+4,
∴E(m,﹣![]() m+4),
m+4),
∴PE=﹣![]() m2+2m,
m2+2m,
∴S△PAC=![]() ×(﹣
×(﹣![]() m2+2m)×6=﹣m2+6m=﹣(m﹣3)2+9,
m2+2m)×6=﹣m2+6m=﹣(m﹣3)2+9,
∵﹣1<0,
∴m=3时,△PAC的面积最大,
∴P(3,5).
(3)∵A(6,0),P(3,5),抛物线y=﹣![]() x2+
x2+![]() x+4的对称轴为直线x=2
x+4的对称轴为直线x=2
∴可设点Q的坐标为(2,m)
∴AQ2=![]()
![]()
PQ2=![]()
![]()
AP2=![]()
①当∠QAP=90°时,则AQ2+AP2= PQ2
即![]() +34=
+34=![]()
解得:m=![]()
∴Q(2,![]() )
)
②当∠AQP=90°时,则AQ2+PQ2= AP2
即![]() +
+![]() =34
=34
解得:m1=1,m2=4
∴Q(2,1)或(2,4)
③当∠QPA=90°时,则AP2+PQ2= AQ2
即34+![]() =
=![]()
解得:m=![]()
∴Q(2,![]() )
)
综上所述,满足条件的点Q坐标为(2,![]() )或(2,
)或(2,![]() )或(2,1)或(2,4).
)或(2,1)或(2,4).