题目内容
在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE=DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.
(1)当点P在线段ED上时(如图1),求证:BE=PD+
PQ;
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.
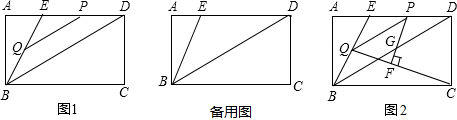
(1)当点P在线段ED上时(如图1),求证:BE=PD+
| ||
| 3 |
(2)若BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与x的函数关系式(不要求写出自变量x的取值范围);
(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长.

(1)证明:∵∠A=90°∠ABE=30°,
∴∠AEB=60°.
∵EB=ED,
∴∠EBD=∠EDB=30°.
∵PQ∥BD,
∴∠EQP=∠EBD.
∠EPQ=∠EDB.
∴∠EPQ=∠EQP=30°,
∴EQ=EP.
过点E作EM⊥QP垂足为M.则PQ=2PM.
∵∠EPM=30°,∴PM=
PE,PE=
PQ.
∵BE=DE=PD+PE,
∴BE=PD+
PQ.
(2)由题意知AE=
BE,
∴DE=BE=2AE.
∵AD=BC=6,
∴2AE=DE=BE=4.
当点P在线段ED上时(如图1),
过点Q做QH⊥AD于点H,则QH=
PQ=
x.
由(1)得PD=BE-
x,PD=4-
x.
∴y=
PD•QH=-
x2+x.
当点P在线段ED的延长线上时(如图2),
过点Q作QH′⊥DA交DA延长线于点H′,
∴QH′=
x.
过点E作EM′⊥PQ于点M′,同理可得EP=EQ=
PQ,
∴BE=
PQ-PD,
∴PD=
x-4,
∴y=
PD•QH′=
x2-x.
(3)连接PC交BD于点N(如图3).
∵点P是线段ED中点,
∴EP=PD=2,PQ=2
.
∵DC=AB=AE•tan60°=2
,
∴PC=
=4.
∴cos∠DPC=
=
.
∴∠DPC=60°.
∴∠QPC=180°-∠EPQ-∠DPC=90°.
∵PQ∥BD,
∴∠PND=∠QPC=90°.
∴PN=
PD=1.
QC=
=2
.
∵∠PGN=90°-∠FPC,∠PCF=90°-∠FPC,
∴∠PGN=∠PCF.
∵∠PNG=∠QPC=90°,
∴△PNG∽△QPC,
∴
=
,
∴PG=
×2
=
.

∴∠AEB=60°.
∵EB=ED,
∴∠EBD=∠EDB=30°.
∵PQ∥BD,
∴∠EQP=∠EBD.
∠EPQ=∠EDB.
∴∠EPQ=∠EQP=30°,
∴EQ=EP.
过点E作EM⊥QP垂足为M.则PQ=2PM.
∵∠EPM=30°,∴PM=
| ||
| 2 |
| ||
| 3 |
∵BE=DE=PD+PE,
∴BE=PD+
| ||
| 3 |
(2)由题意知AE=
| 1 |
| 2 |
∴DE=BE=2AE.
∵AD=BC=6,
∴2AE=DE=BE=4.
当点P在线段ED上时(如图1),
过点Q做QH⊥AD于点H,则QH=
| 1 |
| 2 |
| 1 |
| 2 |
由(1)得PD=BE-
| ||
| 3 |
| ||
| 3 |
∴y=
| 1 |
| 2 |
| ||
| 12 |
当点P在线段ED的延长线上时(如图2),
过点Q作QH′⊥DA交DA延长线于点H′,
∴QH′=
| 1 |
| 2 |
过点E作EM′⊥PQ于点M′,同理可得EP=EQ=
| ||
| 3 |
∴BE=
| ||
| 3 |
∴PD=
| ||
| 3 |
∴y=
| 1 |
| 2 |
| ||
| 12 |
(3)连接PC交BD于点N(如图3).
∵点P是线段ED中点,
∴EP=PD=2,PQ=2
| 3 |
∵DC=AB=AE•tan60°=2
| 3 |
∴PC=
| PD2+DC2 |
∴cos∠DPC=
| PD |
| PC |
| 1 |
| 2 |
∴∠DPC=60°.
∴∠QPC=180°-∠EPQ-∠DPC=90°.
∵PQ∥BD,
∴∠PND=∠QPC=90°.
∴PN=
| 1 |
| 2 |
QC=
| PQ2+PC2 |
| 7 |

∵∠PGN=90°-∠FPC,∠PCF=90°-∠FPC,
∴∠PGN=∠PCF.
∵∠PNG=∠QPC=90°,
∴△PNG∽△QPC,
∴
| PG |
| QC |
| PN |
| PQ |
∴PG=
| 1 | ||
2
|
| 7 |
| ||
| 3 |


练习册系列答案
相关题目
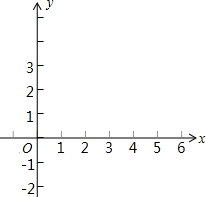
 点B,点C,且BC=4.
点B,点C,且BC=4.
 相等的两部分,求P点的坐标.
相等的两部分,求P点的坐标.
 开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.
开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.