题目内容
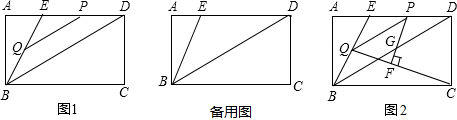
已知,如图,在直角坐标系中,矩形OABC的对角线AC所在直线解析式为y=-
x+1.
(1)在x轴上存在这样的点M,使AMB为等腰三角形,求出所有符合要求的点M的坐标;
(2)动点P从点C开始在线段CO上以每秒
个单位长度的速度向点O移动,同时,动点Q从点O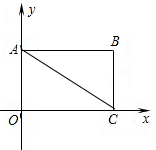 开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.
开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.
①是否存在这样的时刻2,使△OPQ与△BCP相似,并说明理由;
②设△BPQ的面积为S,求S与t间的函数关系式,并求出t为何值时,S有最小值.
| ||
| 3 |
(1)在x轴上存在这样的点M,使AMB为等腰三角形,求出所有符合要求的点M的坐标;
(2)动点P从点C开始在线段CO上以每秒
| 3 |
 开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.
开始在线段OA上以每秒1个单位长度的速度向点A移动.设P、Q移动的时间为t秒.①是否存在这样的时刻2,使△OPQ与△BCP相似,并说明理由;
②设△BPQ的面积为S,求S与t间的函数关系式,并求出t为何值时,S有最小值.
(1)易知A(0,1),C(
,0),B(
,1).
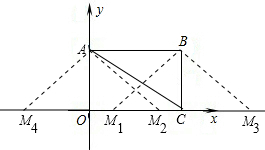
①AB为腰且MA=AB时,
由题意可知,AM2=AB=
,
∴OM2=
.
∴M2(
,0),由对称性知M4(-
,0),
②AB为腰且MB=AB时,
由题意得OM4=OC-CM4=
-
,
∴M1(
-
,0),
由对称性可知M3(
+
,0),
③AB为底边,则M5(
,0);
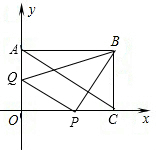 (2)①假设存在这样的时刻t,使△OPQ与△BCP相似.
(2)①假设存在这样的时刻t,使△OPQ与△BCP相似.
∵CP=
t,OQ=t,OP=
-
t,
由
=
或
=
得:
=
或
=
,
即t2+t-1=0或3t=2,
解得t=
或t=
.
又∵0≤t≤1,
∴当t=
或t=
时,△OPQ与△BCP相似.(7分)
②S=S矩形OABC-S△ABQ-S△OPQ-S△BCP
=
-
(1-t)-
t(
-
t)-
•
t
=
(t2-t+1)
=
(t-
)2+
当t=
时,面积S有最小值,最小值是
.(10分)
| 3 |
| 3 |
①AB为腰且MA=AB时,
由题意可知,AM2=AB=
| 3 |
∴OM2=
| 2 |
∴M2(
| 2 |
| 2 |
②AB为腰且MB=AB时,
由题意得OM4=OC-CM4=
| 3 |
| 2 |
∴M1(
| 3 |
| 2 |
由对称性可知M3(
| 3 |
| 2 |
③AB为底边,则M5(
| 1 |
| 2 |
| 3 |
 (2)①假设存在这样的时刻t,使△OPQ与△BCP相似.
(2)①假设存在这样的时刻t,使△OPQ与△BCP相似.∵CP=
| 3 |
| 3 |
| 3 |
由
| OQ |
| BC |
| OP |
| CP |
| OQ |
| CP |
| OP |
| BC |
| t |
| 1 |
| ||||
|
| t | ||
|
| ||||
| t |
即t2+t-1=0或3t=2,
解得t=
-1±
| ||
| 2 |
| 2 |
| 3 |
又∵0≤t≤1,
∴当t=
-1+
| ||
| 2 |
| 2 |
| 3 |
②S=S矩形OABC-S△ABQ-S△OPQ-S△BCP
=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
=
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
当t=
| 1 |
| 2 |
3
| ||
| 8 |


练习册系列答案
相关题目


 面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.