��Ŀ����
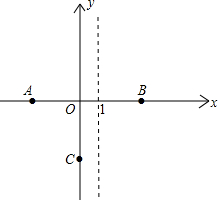
��ͼ��ʾ����֪��ֱ������OABC�У�AB��OC��BC��x���ڵ�C��A��1��1����B��3��1��������P��O���������x����������ÿ��1����λ���ȵ��ٶ��ƶ�����P����PQ��ֱ��ֱ��OA������ΪQ����P���ƶ���ʱ��Ϊt�루0��t��4������OPQ��ֱ������OABC�ص����ֵ����ΪS��
��1����O��A��B����������߽���ʽ��
��2����S��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��t��ʹ����C��P��QΪ��������������OAB���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4������OPQ���ŵ�P˳ʱ����ת90�㣬�Ƿ����t��ʹ�á�OPQ�Ķ���O��Q���������ϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
��1����O��A��B����������߽���ʽ��
��2����S��t�ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��t��ʹ����C��P��QΪ��������������OAB���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4������OPQ���ŵ�P˳ʱ����ת90�㣬�Ƿ����t��ʹ�á�OPQ�Ķ���O��Q���������ϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�

��1���������߽���ʽΪy=ax2+bx��a��0������A��B���������ó���
��
��ã�
��
�ʾ���O��A��B����������߽���ʽΪ��y=-
x2+
x��
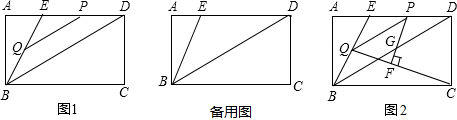
��2���ٵ�0��t��2ʱ���ص�����Ϊ��OPQ������A��AD��x���ڵ�D��
��ͼ1��
��Rt��AOD�У�AD=OD=1����AOD=45�㣮
��Rt��OPQ�У�OP=t����OPQ=��QOP=45�㣮
��OQ=PQ=
t��
��S=S��OPQ=
OQ•PQ=
��
t��
t=
t2��0��t��2����
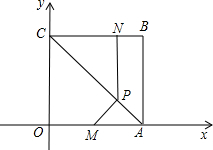
�ڵ�2��t��3ʱ����PQ��AB�ڵ�E���ص�����Ϊ����AOPE��
��EF��x���ڵ�F����ͼ2���ߡ�OPQ=��QOP=45��
���ı���AOPE�ǵ������Ρ�AE=DF=t-2��
��S=S����AOPE=
��AE+OP��•AD=
��t-2+t����1
=t-1��2��t��3����
�۵�3��t��4ʱ����PQ��AB�ڵ�E����BC�ڵ�F��
�ص�����Ϊ�����AOCFE����ͼ3��
��B��3��1����OP=t����PC=CF=t-3��
�ߡ�PFC�͡�BEF���ǵ���ֱ��������
��BE=BF=1-��t-3��=4-t
��S=S�����AOCFE=S����OABC-S��BEF��
=
��2+3����1-
��4-t��2
=-
t2+4t-
��3��t��4����
��3������QC��OB��
��AB��OC��
���BAO+��AOC=180�㣬
�ߡ�AOC=45�㣬��OQP=90�㣬
���QPO=45�㣬
�ߡ�QPO+��QPC=180�㣬
���BAO=��QPC��
ֻҪ
=
����
=
���ɵó���C��P��QΪ��������������OAB���ƣ�
��3-t=
��
t��3-t=
��
t
��ã�t=2��t=
��

��4�����ڣ�t1=1��t2=2��
����OPQ���ŵ�P˳ʱ����ת90�㣬��ʱQ��t+
��
����O��t��t��
�ٵ���Q����������ʱ��
=-
����t+
��2+
����t+
����
���t=2��
�ڵ���O����������ʱ��t=-
t2+
t��
��ã�t=1��

|
��ã�
|
�ʾ���O��A��B����������߽���ʽΪ��y=-
| 1 |
| 3 |
| 4 |
| 3 |
��2���ٵ�0��t��2ʱ���ص�����Ϊ��OPQ������A��AD��x���ڵ�D��
��ͼ1��
��Rt��AOD�У�AD=OD=1����AOD=45�㣮
��Rt��OPQ�У�OP=t����OPQ=��QOP=45�㣮
��OQ=PQ=
| ||
| 2 |
��S=S��OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
�ڵ�2��t��3ʱ����PQ��AB�ڵ�E���ص�����Ϊ����AOPE��

��EF��x���ڵ�F����ͼ2���ߡ�OPQ=��QOP=45��
���ı���AOPE�ǵ������Ρ�AE=DF=t-2��
��S=S����AOPE=
| 1 |
| 2 |
| 1 |
| 2 |
=t-1��2��t��3����
�۵�3��t��4ʱ����PQ��AB�ڵ�E����BC�ڵ�F��
�ص�����Ϊ�����AOCFE����ͼ3��
��B��3��1����OP=t����PC=CF=t-3��
�ߡ�PFC�͡�BEF���ǵ���ֱ��������

��BE=BF=1-��t-3��=4-t
��S=S�����AOCFE=S����OABC-S��BEF��
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 11 |
| 2 |
��3������QC��OB��
��AB��OC��
���BAO+��AOC=180�㣬
�ߡ�AOC=45�㣬��OQP=90�㣬
���QPO=45�㣬
�ߡ�QPO+��QPC=180�㣬
���BAO=��QPC��
ֻҪ
| PC |
| PQ |
| AO |
| AB |
| PC |
| PQ |
| AB |
| AO |
��3-t=
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
��ã�t=2��t=
| 3 |
| 2 |

��4�����ڣ�t1=1��t2=2��
����OPQ���ŵ�P˳ʱ����ת90�㣬��ʱQ��t+
| t |
| 2 |
| t |
| 2 |
�ٵ���Q����������ʱ��
| t |
| 2 |
| 1 |
| 3 |
| t |
| 2 |
| 4 |
| 3 |
| t |
| 2 |
���t=2��
�ڵ���O����������ʱ��t=-
| 1 |
| 3 |
| 4 |
| 3 |
��ã�t=1��


��ϰ��ϵ�д�
 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
�����Ŀ
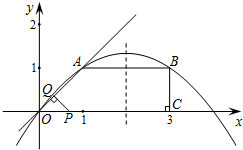
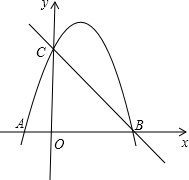
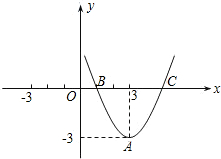 ��������Ե�A��P0��B��CΪ������ı������������֮һ�������ڣ���������з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��������Ե�A��P0��B��CΪ������ı������������֮һ�������ڣ���������з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�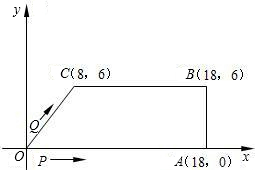

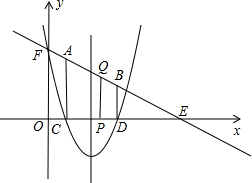 ���ı���PQFC�����S��t֮��ĺ�����ϵʽ����ȷ��t��ȡֵ��Χ��
���ı���PQFC�����S��t֮��ĺ�����ϵʽ����ȷ��t��ȡֵ��Χ��