题目内容

如图，在直角坐标系中，点A的坐标为（-2
3
，0），⊙P刚好与x轴相切于点A，⊙P交y的正半轴于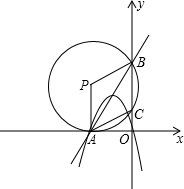点B，点C，且BC=4．
（1）求半径PA的长；
（2）求证：四边形CAPB为菱形；
（3）有一开口向下的抛物线过O，A两点，当它的顶点不在直线AB的上方时，求函数表达式的二次项系数a的取值范围．
（1）作PD⊥BC于D，根据题意PB=
PD2+BD2
=
(2
3
)2+22
=4，
∴半径PA=PB=4．

（2）证明：∵⊙P刚好与x轴相切于点A
∴PA⊥x轴，
∴PA∥BC，
∵PA=BC=4，
∴四边形CAPB是平行四边形．
又∵AP=PB，
∴平行四边形CAPB为菱形．

（3）∵BD=2，
∴点B的坐标为B（0，6），
设直线AB的解析式为y=kx+b则
b=6
-2
3
k+b=0
，
解得
k=
3
b=6
，
∴解析式是y=
3
x+6．
当x=-
3
时，y=3，
此时设抛物线为y=ax2+bx+c，
根据题意
(-2
3
)2a+(-2
3
)b+c=0
c=0

解得b=2
3
a，
∴
4ac-b2
4a
=-3a＜3，
解得a＞-1，
又∵抛物线开口向下，
∴-1＜a＜0．
练习册系列答案
相关题目
如图，在平面直角坐标系中，点O是原点，矩形OABC的顶点A在x轴的正半轴上，顶点C在y的正半轴上，点B的坐标是（5，3），抛物线y=
3
5
x2+bx+c经过A、C两点，与x轴的另一个交点是点D，连接BD．
（1）求抛物线的解析式；
（2）点M是抛物线对称轴上的一点，以M、B、D为顶点的三角形的面积是6，求点M的坐标；
（3）点P从点D出发，以每秒1个单位长度的速度沿D→B匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度沿B→A→D匀速运动，当点P到达点B时，P、Q同时停止运动，设运动的时间为t秒，当t为何值时，以D、P、Q为顶点的三角形是等腰三角形？请直接写出所有符合条件的值．
如图，在直角坐标系中，O是原点，A、B、C三点的坐标分别为A（18，0），B（18，6），C（8，6），四边形OABC是梯形，点P、Q同时从原点出发，分别做匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC、CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动．
（1）求出直线OC的解析式及经过O、A、C三点的抛物线的解析式．
（2）试在（1）中的抛物线上找一点D，使得以O、A、D为顶点的三角形与△AOC全等，请直接写出点D的坐标．
（3）设从出发起，运动了t秒．如果点Q的速度为每秒2个单位，试写出点Q的坐标，并写出此时t的取值范围．
（4）设从出发起，运动了t秒．当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半，这时，直线PQ能否把梯形的面积也分成相等的两部分？如有可能，请求出t的值；如不可能，请说明理由．
已知：如图，二次函数y=ax2+bx+c的图象与x轴、y轴都只有一个交点，分别为A、B且AB=2，又关于x的方程x2-（b+2ac）x+m=0（m＜0）的两个实数根互为相反数．
（1）求ac的值；
（2）求二次函数的解析式；
（3）过A点的直线与二次函数图象相交于另一个点C，与y轴的负半轴相交于点D，且使△ABD和△ABC的面积相等，求此直线的解析式并求△ABC的面积．
如图，已知抛物线y=-
3
4
x2+
9
4
x+3与x轴交于A、B两点（A在B的左侧），与y轴交于点C．
（1）求A、B、C三点的坐标；
（2）求直线BC的函数解析式；
（3）点P是直线BC上的动点，若△POB为等腰三角形，请写出此时点P的坐标．（可直接写出结果）
如图，四边形ABCO是矩形，点A（3，0），B（3，4），动点M、N分别从点O、B出发，以每秒1个单位的速度运动，其中点M沿OA向终点A运动，点N沿BC向终点C运动．过点N作NP∥OC，交AC于点P，连接MP，已知动点运动了x秒，△MPA的面积为S．
（1）求点P的坐标．（用含x的代数式表示）
（2）写出S关于x的函数关系式，并求出S的最大值．
（3）当△APM与△ACO相似时，求出点P的坐标．
（4）△PMA能否成为等腰三角形？如能，直接写出所有点P的坐标；如不能，说明理由．
唐朝诗人李欣的诗《古从军行》开头两句说：“白日登山望峰火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题--将军饮马问题：
如图1所示，诗中将军在观望烽火之后从山脚下的A点出发，走到河旁边的P点饮马后再到B点宿营．请问怎样走才能使总的路程最短？
做法如下：如图1，从B出发向河岸引垂线，垂足为D，在AD的延长线上，取B关于河岸的对称点B′，连接AB′，与河岸线相交于P，则P点就是饮马的地方，将军只要从A出发，沿直线走到P，饮马之后，再由P沿直线走到B，所走的路程就是最短的．
（1）观察发现
再如图2，在等腰梯形ABCD中，AB=CD=AD=2，∠D=120°，点E、F是底边AD与BC的中点，连接EF，在线段EF上找一点P，使BP+AP最短．
作点B关于EF的对称点，恰好与点C重合，连接AC交EF于一点，则这点就是所求的点P，故BP+AP的最小值为______．
（2）实践运用
如图3，已知⊙O的直径MN=1，点A在圆上，且∠AMN的度数为30°，点B是弧AN的中点，点P在直径MN上运动，求BP+AP的最小值．
（3）拓展迁移
如图4，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．
①求这条抛物线所对应的函数关系式；
②在抛物线的对称轴直线x=1上找到一点M，使△ACM周长最小，请求出此时点M的坐标与△ACM周长最小值．（结果保留根号）
问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2(x+
a
x
)(x＞0)．
探索研究
（1）我们可以借鉴学习函数的经验，先探索函数y=x+
1
x
(x＞0)的图象性质．
1填写下表，画出函数的图象：
x…
1
4
1
3
1
2
1234…
y……
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，除了通过观察图象，还可以通过配方得到．同样通过配方也可以求函数y=x+
1
x
（x＞0）的最小值．y=x+
1
x
=(
x
)2+(
1
x
)2=(
x
)2+(
1
x
)2-2
x
•
1
x
+2
x
•
1
x

=(
x
-
1
x
)2+2≥2
当
x
-
1
x
=0，即x=1时，函数y=x+
1
x
（x＞0）的最小值为2．
解决问题
（2）解决“问题情境”中的问题，直接写出答案．
在矩形ABCD中，点E是AD边上一点，连接BE，且∠ABE=30°，BE=DE，连接BD．点P从点E出发沿射线ED运动，过点P作PQ∥BD交直线BE于点Q．
（1）当点P在线段ED上时（如图1），求证：BE=PD+
3
3
PQ；
（2）若BC=6，设PQ长为x，以P、Q、D三点为顶点所构成的三角形面积为y，求y与x的函数关系式（不要求写出自变量x的取值范围）；
（3）在②的条件下，当点P运动到线段ED的中点时，连接QC，过点P作PF⊥QC，垂足为F，PF交对角线BD于点G（如图2），求线段PG的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网