题目内容
如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.
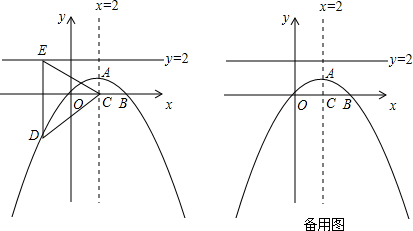
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2,并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.

(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2,并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
(1)依题意,设抛物线的解析式为:y=a(x-2)2+1,代入B(4,0),得:
a(4-2)2+1=0,解得:a=-
∴抛物线的解析式:y=-
(x-2)2+1.
(2)①猜想:CD2=DE2;
证明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x-2)2+y2,DE2=(y-2)2;
由(1)知:(x-2)2=-4(y-1)=-4y+4,代入CD2中,得:
CD2=y2-4y+4=(y-2)2=DE2.
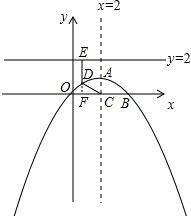 ②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
延长ED交x轴于F,则EF⊥x轴;
在Rt△CDF中,∠FDC=180°-120°=60°,∠DCF=30°,则:
CD=2DF、CF=
DF;
设DF=m,则:CF=
m、CD=DE=2m;
∵EF=ED+DF=2m+m=2,
∴m=
,DF=m=
,CF=
m=
,OF=OC-CF=2-
,
∴D(2-
,
);
同理,抛物线对称轴右侧有:D(2+
,
);
综上,存在符合条件的D点,且坐标为(2-
,
)或(2+
,
).
a(4-2)2+1=0,解得:a=-
| 1 |
| 4 |
∴抛物线的解析式:y=-
| 1 |
| 4 |
(2)①猜想:CD2=DE2;
证明:由D(x,y)、C(2,0)、E(x,2)知:
CD2=(x-2)2+y2,DE2=(y-2)2;
由(1)知:(x-2)2=-4(y-1)=-4y+4,代入CD2中,得:
CD2=y2-4y+4=(y-2)2=DE2.
 ②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:
②由于∠EDC=120°>90°,所以点D必在x轴上方,且抛物线对称轴左右两侧各有一个,以左侧为例:延长ED交x轴于F,则EF⊥x轴;
在Rt△CDF中,∠FDC=180°-120°=60°,∠DCF=30°,则:
CD=2DF、CF=
| 3 |
设DF=m,则:CF=
| 3 |
∵EF=ED+DF=2m+m=2,
∴m=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∴D(2-
2
| ||
| 3 |
| 2 |
| 3 |
同理,抛物线对称轴右侧有:D(2+
2
| ||
| 3 |
| 2 |
| 3 |
综上,存在符合条件的D点,且坐标为(2-
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |

练习册系列答案
相关题目



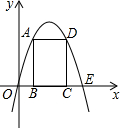
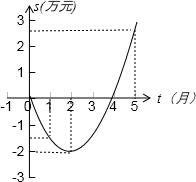 来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: