Question

在平面直角坐标系xOy中，已知直线y=-

3

3

x+

2 3

3

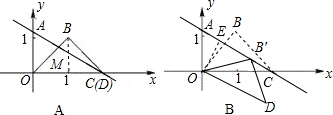
交x轴于点C，交y轴于点A．等腰直角三角板OBD的顶点D与点C重合，如图A所示．把三角板绕着点O顺时针旋转，旋转角度为α（0°＜α＜180°），使B点恰好落在AC上的B'处，如图B所示．
（1）求图A中的点B的坐标；
（2）求α的值；
（3）若二次函数y=mx²+3x的图象经过（1）中的点B，判断点B′是否在这条抛物线上，并说明理由．

Answer 1

（1）∵直线y=-

3

3

x+

2 3

3

交x轴于点C，交y轴于点A，
∴点A的坐标为（0，

2 3

3

），点C的坐标为（2，0）．
∵等腰直角三角板OBD的顶点D与点C重合，
∴OD=2，∠BOD=45°．
过点B作BM⊥OC于M．
∴OM=

1

2

OD=1．
∴BM=1，OB=

2

．
∴点B的坐标为（1，1）

（2）∵OA=

2 3

3

，OC=2，∠AOC=90°，
∴∠ACO=30°．
过点O作OE⊥AC于E．
∴OE=1．
∵在Rt△B′EO中，OB′=

2

，OE=1，
∴∠B′OE=45°．
∴∠EOD=90°．
又∵∠EOC=60°，
∴∠COD=30°．
∴α=30°．

（3）判断：点B'在这条抛物线上．
理由：∵点B'在直线AC上，
∴点B'的坐标为（a，-

3

3

a+

2 3

3

）．
∵a²+（-

3

3

a+

2 3

3

）²=OB'²，
∴a²+（-

3

3

a+

2 3

3

）²=（

2

）²．
解方程，得a₁=

1+ 3

2

，a₂=

1- 3

2

（不合题意，舍去）．
∴点B'的坐标为（

1+ 3

2

，

3 -1

2

）．
又∵二次函数y=mx²+3x过B（1，1），
∴m=-2．
∴二次函数的解析式为y=-2x²+3x．把x=

1+ 3

2

代入y=-2x²+3x，得y=

3 -1

2

∴点B'在这条抛物线上．
（注：对于每题的不同解法，请老师们根据评分标准酌情给分．）