题目内容

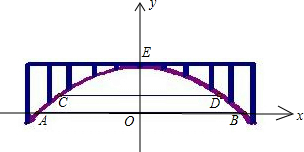
如图，有一座抛物线形的拱桥，桥下面处在目前的水位时，水面宽AB=10m，如果水位上升2m，就将达到警戒线CD，这时水面的宽为8m．若洪水到来，水位以每小时0.1m速度上升，经过多少小时会达到拱顶？
以AB所在的直线为x轴，AB中点为原点，建立直角坐标系，
则抛物线的顶点E在y轴上，且B、D两点的坐标分别为（5，0）、（4，2）
设抛物线为y=ax2+k
由B、D两点在抛物线上，有
16a+k=2
25a+k=0

解这个方程组，得a=-
2
9
，k=
50
9
，
所以，y=-
2
9
x2+
50
9
，
其顶点的坐标为（0，
50
9
），
则OE=
50
9

50
9
÷0.1=
500
9
（h）．
所以，若洪水到来，水位以每小时0.1m速度上升，经过
500
9
小时会达到拱顶．
练习册系列答案
相关题目
如图，四边形ABCO是矩形，点A（3，0），B（3，4），动点M、N分别从点O、B出发，以每秒1个单位的速度运动，其中点M沿OA向终点A运动，点N沿BC向终点C运动．过点N作NP∥OC，交AC于点P，连接MP，已知动点运动了x秒，△MPA的面积为S．
（1）求点P的坐标．（用含x的代数式表示）
（2）写出S关于x的函数关系式，并求出S的最大值．
（3）当△APM与△ACO相似时，求出点P的坐标．
（4）△PMA能否成为等腰三角形？如能，直接写出所有点P的坐标；如不能，说明理由．
如图已知二次函数图象的顶点为原点，直线y=
1
2
x+4的图象与该二次函数的图象交于A点（8，8），直线与x轴的交点为C，与y轴的交点为B．
（1）求这个二次函数的解析式与B点坐标；
（2）P为线段AB上的一个动点（点P与A，B不重合），过P作x轴的垂线与这个二次函数的图象交于D点，与x轴交于点E．设线段PD的长为h，点P的横坐标为t，求h与t之间的函数关系式，并写出自变量t的取值范围；
（3）在（2）的条件下，在线段AB上是否存在点P，使得以点P、D、B为顶点的三角形与△BOC相似？若存在，请求出P点的坐标；若不存在，请说明理由．
如图，在同一直角坐标系内，如果x轴与一次函数y=kx+4的图象以及分别过C（1，0）、D（4，0）两点且平行于y轴的两条直线所围成的图形ABDC的面积为7．
（1）求k的值；
（2）求过F、C、D三点的抛物线的解析式；
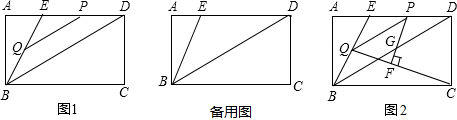
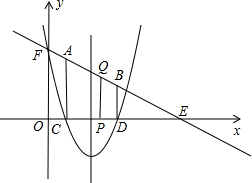（3）线段CD上的一个动点P从点D出发，以1单位/秒的速度沿DC的方向移动（点P不重合于点C），过P点作直线PQ⊥CD交EF于Q．当P从点D出发t秒后，求四边形PQFC的面积S与t之间的函数关系式，并确定t的取值范围．
如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（6，0），（6，8）．动点M、N分别从O、B同时出发，以每秒1个单位的速度运动．其中，点M沿OA向终点A运动，点N沿BC向终点C运动．过点N作NP⊥BC，交AC于P，连接MP．已知动点运动了x秒．
（1）P点的坐标为多少；（用含x的代数式表示）
（2）试求△MPA面积的最大值，并求此时x的值；
（3）请你探索：当x为何值时，△MPA是一个等腰三角形？你发现了几种情况？写出你的研究成果．
唐朝诗人李欣的诗《古从军行》开头两句说：“白日登山望峰火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题--将军饮马问题：
如图1所示，诗中将军在观望烽火之后从山脚下的A点出发，走到河旁边的P点饮马后再到B点宿营．请问怎样走才能使总的路程最短？
做法如下：如图1，从B出发向河岸引垂线，垂足为D，在AD的延长线上，取B关于河岸的对称点B′，连接AB′，与河岸线相交于P，则P点就是饮马的地方，将军只要从A出发，沿直线走到P，饮马之后，再由P沿直线走到B，所走的路程就是最短的．
（1）观察发现
再如图2，在等腰梯形ABCD中，AB=CD=AD=2，∠D=120°，点E、F是底边AD与BC的中点，连接EF，在线段EF上找一点P，使BP+AP最短．
作点B关于EF的对称点，恰好与点C重合，连接AC交EF于一点，则这点就是所求的点P，故BP+AP的最小值为______．
（2）实践运用
如图3，已知⊙O的直径MN=1，点A在圆上，且∠AMN的度数为30°，点B是弧AN的中点，点P在直径MN上运动，求BP+AP的最小值．
（3）拓展迁移
如图4，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．
①求这条抛物线所对应的函数关系式；
②在抛物线的对称轴直线x=1上找到一点M，使△ACM周长最小，请求出此时点M的坐标与△ACM周长最小值．（结果保留根号）
问题情境
已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2(x+
a
x
)(x＞0)．
探索研究
（1）我们可以借鉴学习函数的经验，先探索函数y=x+
1
x
(x＞0)的图象性质．
1填写下表，画出函数的图象：
x…
1
4
1
3
1
2
1234…
y……
②观察图象，写出该函数两条不同类型的性质；
③在求二次函数y=ax2+bx+c（a≠0）的最大（小）值时，除了通过观察图象，除了通过观察图象，还可以通过配方得到．同样通过配方也可以求函数y=x+
1
x
（x＞0）的最小值．y=x+
1
x
=(
x
)2+(
1
x
)2=(
x
)2+(
1
x
)2-2
x
•
1
x
+2
x
•
1
x

=(
x
-
1
x
)2+2≥2
当
x
-
1
x
=0，即x=1时，函数y=x+
1
x
（x＞0）的最小值为2．
解决问题
（2）解决“问题情境”中的问题，直接写出答案．
在矩形ABCD中，点E是AD边上一点，连接BE，且∠ABE=30°，BE=DE，连接BD．点P从点E出发沿射线ED运动，过点P作PQ∥BD交直线BE于点Q．
（1）当点P在线段ED上时（如图1），求证：BE=PD+
3
3
PQ；
（2）若BC=6，设PQ长为x，以P、Q、D三点为顶点所构成的三角形面积为y，求y与x的函数关系式（不要求写出自变量x的取值范围）；
（3）在②的条件下，当点P运动到线段ED的中点时，连接QC，过点P作PF⊥QC，垂足为F，PF交对角线BD于点G（如图2），求线段PG的长．
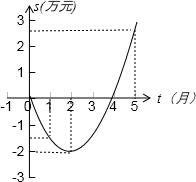为了顺应市场要求，某市电子玩具制造公司技术部研制开发一种新产品，年初上市后，公司经历了从亏损到盈利的过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s和t之间的关系）．根据图象提供的信息，解答下列问题：
（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到几月末公司累积利润可达到6万元？
（3）求第9个月公司所获利润是多少万元？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网