题目内容
在梯形纸片ABCD中，AD//BC，AD＞CD. 将纸片沿过点D的直线折叠，使点C落在AD边上的点C′处，折痕DE交BC于点E，连接C′E，则四边形CDC′E的形状准确地说应为（■）.
A.矩形 B. 菱形
C. 梯形 D. 平行四边形
A.矩形 B. 菱形
C. 梯形 D. 平行四边形
B
四边形CDC′E是菱形．
理由：根据折叠的性质，可得：CD=C′D，∠C′DE=∠CDE，CE=C′E，
∵AD∥BC，
∴∠C′DE=∠CED，
∴∠CDE=∠CED，
∴CD=CE，
∴CD=C′D=C′E=CE，
∴四边形CDC′E为菱形．
故选B．
理由：根据折叠的性质，可得：CD=C′D，∠C′DE=∠CDE，CE=C′E，
∵AD∥BC，
∴∠C′DE=∠CED，
∴∠CDE=∠CED，
∴CD=CE，
∴CD=C′D=C′E=CE，
∴四边形CDC′E为菱形．
故选B．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
∠BAD.求证:EF＝BE＋FD;
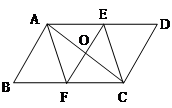
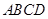中，对角线
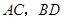交于点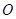
， 已知∠AOD=120°，AB=3,则
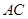的长为 ▲ .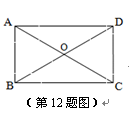
是平行四边形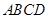
的对角线
为圆心，以大于
长为半径画弧，弧在
；
分别与
交于点
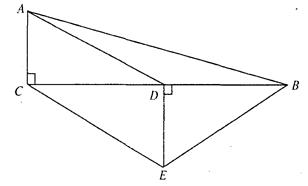
满分6分）如图，在△ABC中，∠ACB＝90°，D是BC中点，DE⊥BC，CE∥AD，若AC＝2，CE＝4．求四边形ACEB的周长．