题目内容
如图，已知E、F、G、H是四边形ABCD四边的中点，则四边形EFGH的形状为■；如四边形ABCD的对角线AC 与BD的和为40，则四边形EFGH的周长为■.
平行四边形； 40
利用三角形的中位线定理求出四边形EFGH的两组对边相等，即可证得四边形EFGH是平行四边形，继而即可求得EFGH的周长．
解：连接AC、BD，
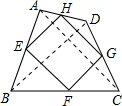
∵E、F、G、H分别为四边形ABCD四边的中点，
∴EH=
BD，FG=BD，HG=AC，EF=AC，
∴EH=FG，EF=HG，
∴四边形EFGH是平行四边形．
∴四边形EFGH的周长=EH+HG+FG+EF=×2×AC+×2×BD=AC+BD=40．
故答案为：平行四边形；40．
解：连接AC、BD，
∵E、F、G、H分别为四边形ABCD四边的中点，
∴EH=
BD，FG=BD，HG=AC，EF=AC，∴EH=FG，EF=HG，
∴四边形EFGH是平行四边形．
∴四边形EFGH的周长=EH+HG+FG+EF=
×2×AC+×2×BD=AC+BD=40．故答案为：平行四边形；40．
练习册系列答案
相关题目
