Question

【题目】如图，⊙O的半径为（r＞0），若点P′在射线OP上（P′可以和射线端点重合），满足OP′+OP＝2r，则称点P′是点P关于⊙O的“反演点”．

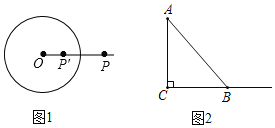
（1）当⊙O的半径为8时，

①若OP1＝17，OP2＝12，OP3＝4，则P1，P2，P3中存在关于⊙O的反演点”的是　 　．

②点O关于⊙O的“反演点”的集合是　 　，若P关于⊙O的“反演点在⊙O内，则OP取值范围是　 　；

（2）如图2，△ABC中，∠ACB＝90°，AC＝BC＝12，⊙O的圆心在射线CB上运动，半径为1．若线段AB上存在点P，使得点P关于⊙O的“反演点”P′在⊙O的内部，求OC的取值范围．

Answer 1

【答案】（1）①P2，P3；②以O为圆心，半径为16的圆，8＜OP≤16；（2）当12﹣2≤OC≤14时，线段AB上存在点P，使得点P关于⊙O的“反演点”P′在⊙O的内部．

【解析】

（1）①、②运用“反演点”的定义进行解答即可；

（2）需分两种情形讨论①当点O在线段CB上时，以O为圆心，半径为2的圆与AB相切于H，确定OC的范围即可；②当点O在点B右侧时，确定OC的范围即可；

解：（1）①根据⊙O的“反演点”的定义可知：当0≤OP≤2r时，点P存在关于⊙O的“反演点”，

∵OP1＝17，OP2＝12，OP3＝4，

∴P2，P3存在关于⊙O的“反演点”，

故答案为P2，P3．

②点O关于⊙O的“反演点”的集合是以O为圆心，半径为16的圆，若P关于⊙O的“反演点在⊙O内，则OP取值范围是

故答案为：以O为圆心，半径为16的圆；8＜OP≤16；

（2）①当点O在线段CB 上时，以O为圆心，半径为2的圆与AB相切于H，如图，

这时OC＝CB﹣OB＝12﹣2，此时线段AB上存在点P（即为点H），使得点P关于⊙O的“反演点”P′在⊙O的内部，即为圆心O，当图中点O向点B靠近时，线段AB上必存在着点P，使得OP≤2，又OP+O P′＝2，

∴O P′＜1，即点P关于⊙O的“反演点”P′在⊙O的内部．

∴12﹣2≤OC≤12

②当点O在点B右侧时，

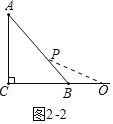
∵OP≥OB，又1＜OP≤2，

∴0＜OB≤2，

∴12＜OC≤14，

综上所述，当12﹣2≤OC≤14时，线段AB上存在点P，使得点P关于⊙O的“反演点”P′在⊙O的内部．