Question

【题目】在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线．

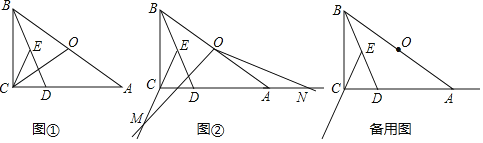
（1）如图①，连接OC，证明∠OCE＝∠OAC；

（2）如图②，点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N．

①猜想并证明线段OM和线段ON之间的数量关系；

②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度（用含m的式子表示）．

Answer 1

【答案】（1）见解析；（2）①OM＝ON，证明见解析；②满足条件的EM的值为m+m或m﹣m

【解析】

（1）根据是Rt△ABC斜边是的中线，可证得∠OCA＝∠A，根据是Rt△DBC斜边是的中线， 是△DBA的中位线，可证得∠EOC＝∠OCA＝∠ECO，从而得到结论；

（2）①连接，和△DBA有一个底角相等的等腰三角形，得到∠COA＝∠ADB，继而得到∠COM＝∠AON，可证得△COM≌△AON（ASA），继而证得结论；

②分类讨论：当点N在CA的延长线上时，利用外角定理得∠AON＝∠ANO＝15°，OA＝AN＝m，根据△OCM≌△OAN，得到CM＝AN＝m，在Rt△BCD中，求得，继而求得答案；当点N在线段AC上时，作OH⊥AC于H，求得OH＝HN＝m， AH＝m，继而求得答案.

（1）证明：如图①中，连接OE．

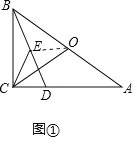
∵∠BCD＝90°，BE＝ED，BO＝OA，

∵CE＝ED＝EB＝BD，CO＝OA＝OB，

∴∠OCA＝∠A，

∵BE＝ED，BO＝OA，

∴OE∥AD，OE＝AD，

∴CE＝EO．

∴∠EOC＝∠OCA＝∠ECO，

∴∠ECO＝∠OAC．

故答案为：∠OCE＝∠OAC．

（2）①如图，连接，

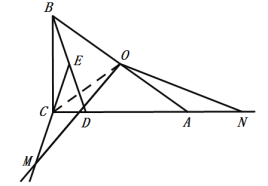
∵OC＝OA，DA＝DB，

∴∠＝∠OCA＝∠ABD，

∴∠COA＝∠ADB，

∵∠MON＝∠ADB，

∴∠AOC＝∠MON，

∴∠COM＝∠AON，

∵∠ECO＝∠OAC，

∴∠MCO＝∠NAO，

∵OC＝OA，

∴△COM≌△AON（ASA），

∴OM＝ON．

②如图，当点N在CA的延长线上时，

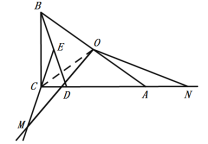
∵∠CAB＝30°＝∠OAN+∠ANO，∠AON＝15°，

∴∠AON＝∠ANO＝15°，

∴OA＝AN＝m，

∵△OCM≌△OAN，

∴CM＝AN＝m，

在Rt△BCD中，∵BC＝m，∠CDB＝60°，

∴BD＝m，

∵BE＝ED，

∴CE＝BD＝m，

∴EM＝CM+CE＝m+m．

如图中，当点N在线段AC上时，作OH⊥AC于H．

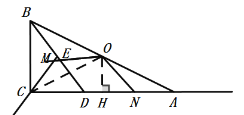
∵∠AON＝15°，∠CAB＝30°，

∴∠ONH＝15°+30°＝45°，

∴OH＝HN＝m，

∵AH＝m，

∴CM＝AN＝m﹣m，

∵EC＝m，

∴EM＝EC﹣CM＝m﹣（m﹣m）＝m﹣m，

综上所述，满足条件的EM的值为m+m或m﹣m．