Question

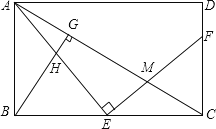
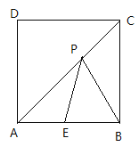
【题目】如图正方形ABCD中,E为AB中点,P为对角线AC上一点，且PB+PE=,则正方形ABCD边长的最大值是_____．

Answer 1

【答案】2

【解析】

如下图，作点E关于AC的对称点F，连接FB，直线FB与AC的交点为点G，当点P与点G重合时，正方形ABCD的边长最长，根据勾股定理可求得．

如下图，作点E关于AC的对称点F，连接FB，直线FB与AC的交点为点G，连接FP

∵四边形ABCD是正方形，点E是AB的中点

∴根据正方形的性质，点F为AD的中点

∵点F是点E关于AC的对称点

∴EP=FP

∵EP+PB是定值

∴FP+PB是定值

在△FPB中，FP+PB≥FB

∴当点P与点G重合时，FB最大，FB=FP+PB=

则此刻，正方形ABCD的边长最大，设边长为2a

则AB=2a，AF=a

在Rt△ABF中，

解得：a=1

∴正方形的边长为2

故答案为：2．