题目内容
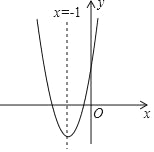
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的解析式.
(2)点P是线段BC下方抛物线上的一个动点.
①求四边形PBAC面积的最大值,并求四边形PBAC面积的最大时P点的坐标;
②如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形是平行四边形.求点Q的坐标.

【答案】(1)![]() x2﹣x﹣4,
x2﹣x﹣4,![]() ;(2)①16;②点Q的坐标为(2,0)或(6,0)
;(2)①16;②点Q的坐标为(2,0)或(6,0)
【解析】
(1)先根据题意确定点A、B、C的坐标,然后用待定系数法即可解答;
(2)①过P作x轴的垂线交直线BC于点N,连接PC,PB.设P(x,![]() x2﹣x﹣4),N(x,x-4).再用x表示出PN的长度,然后根据二次函数性质求出PN的最大值,进而求得
x2﹣x﹣4),N(x,x-4).再用x表示出PN的长度,然后根据二次函数性质求出PN的最大值,进而求得![]() 的最大值,最后再加上
的最大值,最后再加上![]() 即可解答;②以BC为平行四边形的一边和以BC为平行四边形的对角线两种情况讨论,利用平移和中点公式进行求解即可.
即可解答;②以BC为平行四边形的一边和以BC为平行四边形的对角线两种情况讨论,利用平移和中点公式进行求解即可.
解:(1)由点A、B、C在抛物线y![]() x2﹣x﹣4的函数图像上
x2﹣x﹣4的函数图像上
令y=0,则x=4或﹣2,即点A、B的坐标分别为(﹣2,0)、(4,0);
令x=0时,y=-4,即C点坐标(0,-4).
由待定系数法可得直线BC的解析式为:y=x-4.
(2)
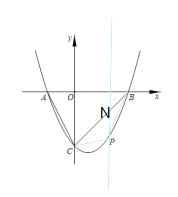
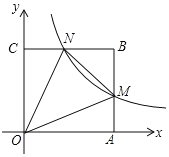
①如图,过P作x轴的垂线交直线BC于点N,连接PC,PB.
设P(x,![]() x2﹣x﹣4),N(x,x-4).
x2﹣x﹣4),N(x,x-4).
∴PN=x-4-(![]() x2﹣x﹣4)=-
x2﹣x﹣4)=-![]() x2+2x=-
x2+2x=-![]() (x-2)2-2
(x-2)2-2
∴当x=2时,PN有最大值为2.此时P坐标为(2,-4).
∴![]() =
=![]() PN·OB=
PN·OB=![]() ×2×4=4
×2×4=4
∴四边形PBAC面积最大值=![]() =12+4=16
=12+4=16
② 第一种情况:当BC是平行四边形的一条边时,
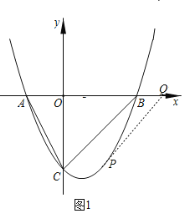
如图所示,点C向右平移4个单位、向上平移4个单位得到点B,
设:点P(n,![]() n2﹣n﹣4),点Q(m,0),
n2﹣n﹣4),点Q(m,0),
则点P向右平移4个单位、向上平移4
即:n+4=m,![]() n2﹣n﹣4+4=0,
n2﹣n﹣4+4=0,
解得:m=4或6(舍去4),
即点Q(6,0);
第二种情况:当BC是平行四边形的对角线时,
设点P(m,n)、点Q(s,0),其中n![]() m2﹣m﹣4,
m2﹣m﹣4,
由中点公式可得:m+s=﹣2,n+0=4,
解得:s=2或4(舍去4),
故点Q(2,0);
故点Q的坐标为(2,0)或(6,0);

【题目】经历疫情复学后,学校开展了多种形式的防疫知识讲座,并举行了全员参加的“防疫”知识竞赛,试卷题目共10题,每题10分.现分别从七年级1,2,3班中各随机抽取10名同学的成绩(单位:分).
收集整理数据如下:
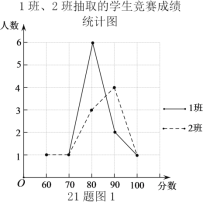
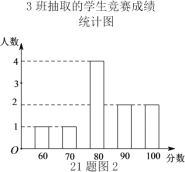
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 |
| 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(一条理由即可);
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级学生共120人,试估计需要准备多少张奖状?
【题目】2020年春,受疫情影响,同学们进行了3个多月的网课迎来了复学,为了解九年级学生网课期间学习情况,学校在复学后进行了复学测试,小虎同学在九年级随机抽取了一部分学生的复学测试数学成绩为样本,分为A(100~90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
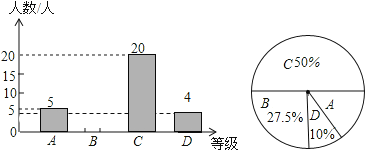
其中C组的期末数学成绩如下:
61 | 63 | 65 | 66 | 66 | 67 | 69 | 70 | 72 | 73 |
75 | 75 | 76 | 77 | 77 | 77 | 78 | 78 | 79 | 79 |
(1)请补全条形统计图;
(2)扇形统计图中A组所占的圆心角的度数为______,C组的复学测试数学成绩的中位数是______,众数是_______;
(3)这个学校九年级共有学生400人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生复学测试数学考试成绩为优秀的学生人数大约有多少?