题目内容
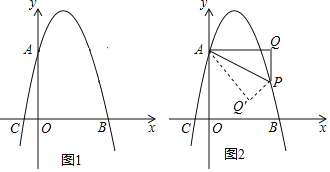
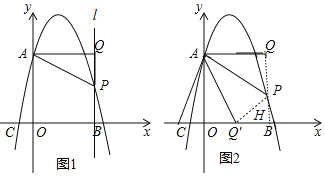
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
【答案】(1)y=﹣x2+3x+4;(﹣1,0);(2)P的横坐标为![]() 或
或![]() .(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
.(3)点P的坐标为(4,0)或(5,﹣6)或(2,6).
【解析】
(1)利用待定系数法求抛物线解析式,然后利用抛物线解析式得到一元二次方程,通过解一元二次方程得到C点坐标;
(2)利用△AQP∽△AOC得到AQ=4PQ,设P(m,﹣m2+3m+4),所以m=4|4﹣(﹣m2+3m+4|,然后解方程4(m2﹣3m)=m和方程4(m2﹣3m)=﹣m得P点坐标;
(3)设P(m,﹣m2+3m+4)(m>![]() ),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
),当点Q′落在x轴上,延长QP交x轴于H,如图2,则PQ=m2﹣3m,证明Rt△AOQ′∽Rt△Q′HP,利用相似比得到Q′B=4m﹣12,则OQ′=12﹣3m,在Rt△AOQ′中,利用勾股定理得到方程42+(12﹣3m)2=m2,然后解方程求出m得到此时P点坐标;当点Q′落在y轴上,易得点A、Q′、P、Q所组成的四边形为正方形,利用PQ=PQ′得到|m2﹣3m|=m,然后解方程m2﹣3m=m和方程m2﹣3m=﹣m得此时P点坐标.
解:(1)把A(0,4),B(4,0)分别代入y=﹣x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+3x+4,
当y=0时,﹣x2+3x+4=0,解得x1=﹣1,x2=4,
∴C(﹣1,0);
故答案为y=﹣x2+3x+4;(﹣1,0);
(2)∵△AQP∽△AOC,
∴![]() ,
,
∴![]() ,即AQ=4PQ,
,即AQ=4PQ,
设P(m,﹣m2+3m+4),
∴m=4|4﹣(﹣m2+3m+4|,即4|m2﹣3m|=m,
解方程4(m2﹣3m)=m得m1=0(舍去),m2=![]() ,此时P点横坐标为
,此时P点横坐标为![]() ;
;
解方程4(m2﹣3m)=﹣m得m1=0(舍去),m2=![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
综上所述,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)设![]() ,
,
当点Q′落在x轴上,延长QP交x轴于H,如图2,
则PQ=4﹣(﹣m2+3m+4)=m2﹣3m,
∵△APQ沿AP对折,点Q的对应点为点Q',
∴∠AQ′P=∠AQP=90°,AQ′=AQ=m,PQ′=PQ=m2﹣3m,
∵∠AQ′O=∠Q′PH,
∴Rt△AOQ′∽Rt△Q′HP,
∴![]() ,即
,即![]() ,解得Q′H=4m﹣12,
,解得Q′H=4m﹣12,
∴OQ′=m﹣(4m﹣12)=12﹣3m,
在Rt△AOQ′中,42+(12﹣3m)2=m2,
整理得m2﹣9m+20=0,解得m1=4,m2=5,此时P点坐标为(4,0)或(5,﹣6);
当点Q′落在y轴上,则点A、Q′、P、Q所组成的四边形为正方形,
∴PQ=AQ′,
即|m2﹣3m|=m,
解方程m2﹣3m=m得m1=0(舍去),m2=4,此时P点坐标为(4,0);
解方程m2﹣3m=﹣m得m1=0(舍去),m2=2,此时P点坐标为(2,6),
综上所述,点P的坐标为(4,0)或(5,﹣6)或(2,6)

 阅读快车系列答案
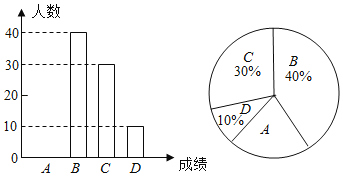
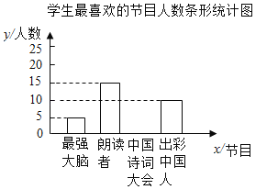
阅读快车系列答案【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随杋抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
学生最喜爱的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | |
中国诗词大会 |
| 40% |
出彩中国人 | 10 | 20% |
根据以上信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全上面的条形统计图;
(3)若该校共有学生![]() 名,估计该校学生最喜爱《朗读者》节目的人数.
名,估计该校学生最喜爱《朗读者》节目的人数.
【题目】经历疫情复学后,学校开展了多种形式的防疫知识讲座,并举行了全员参加的“防疫”知识竞赛,试卷题目共10题,每题10分.现分别从七年级1,2,3班中各随机抽取10名同学的成绩(单位:分).
收集整理数据如下:
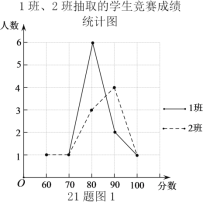
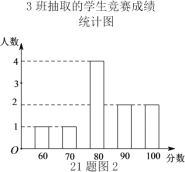
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 |
| 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(一条理由即可);
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级学生共120人,试估计需要准备多少张奖状?