题目内容
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图①.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图②,当∠COD在∠AOB的外部时,
①请直接写出∠AOC与∠DOE的度数之间的关系;
②在∠AOC内部有一条射线OF,满足∠AOC+2∠BOE=4∠AOF,写出∠AOF与∠DOE的度数之间的关系.
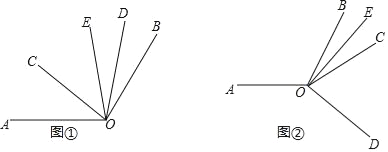
【答案】(1)①19°50′;②∠DOE=![]() ;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
【解析】
(1)①②根据角平分线的定义和角的和差即可得到结论;
②根据角平分线的定义和角的和差即可得到结论;
(2)①根据已知条件得到∠AOC=120°+∠BOC,∠DOE=60°+∠COE,根据角平分线的定义得到∠COE=![]() ∠BOC,等量代换即可得到结论;
∠BOC,等量代换即可得到结论;
②如图,由①知,∠AOC=2∠DOE,根据∠AOC+2∠BOE=4∠AOF,化简即可得到结论.
(1)①∵∠AOB=120°,∠COD=60°,∠AOC=39°40′,
∴∠BOC=∠AOB﹣∠AOC=120°﹣39°40′=80°20′,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=40°10′,
∠BOC=40°10′,
∴∠DOE=∠COD﹣∠COE=19°50′;
②∵∠AOB=120°,∠COD=60°,∠AOC=α,
∴∠BOC=∠AOB﹣∠AOC=120°﹣α,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°﹣
∠BOC=60°﹣![]() α,
α,
∴∠DOE=![]() ;
;
(2)①∵∠AOC=120°+∠BOC,∠DOE=60°+∠COE,
∵OE平分∠BOC,
∴∠COE=![]() BOC,
BOC,
∴∠AOC=2∠DOE;
②如图,
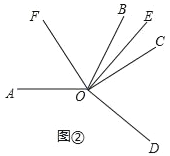
由①知,∠AOC=2∠DOE,
∵∠AOC+2∠BOE=4∠AOF,
∴∠AOC+∠BOC=∠AOC+∠AOC﹣120°=2∠AOC﹣120°=4∠DOE﹣120°=4∠AOF,
∴∠DOE=∠AOF+30°.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案