题目内容
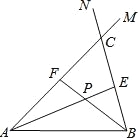
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】首先根据折叠可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,进而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
从而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的长.
,在Rt△B/DF中,由勾股定理即可求得B/F的长.
解:根据首先根据折叠可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案为: ![]()
“点睛”此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等,根据折叠的性质求得相等的角是解本题的关键.

【题目】今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.0 | 20.5 | 21.0 | 21.5 |
(1)请建立该水库水位y(米)与日期x之间的函数模型,求出函数表达式;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?请简要说明.