题目内容
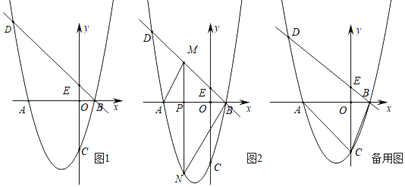
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 轴,且直线l与抛物线
轴,且直线l与抛物线![]() 和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为
和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为![]() ,点A的横坐标为1.
,点A的横坐标为1.
(1)线段AB的长度等于________;
(2)点P为线段AB上方抛物线上的一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() 的面积最大时,求
的面积最大时,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,删除抛物线![]() 在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线
在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线![]() ,若直线
,若直线![]() 与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
【答案】(1)2 (2) ![]() (3) t的取值范围为:t<
(3) t的取值范围为:t<![]() .
.
【解析】
(1)先求抛物线y=-x2+4x的对称轴,由于已知点A的坐标,再利用对称性可求点B坐标;从而得AB的长度;
(2)先根据B和E坐标得出BE的解析式,然后设与其平行的直线为y=x+b,过点H作y=-x的垂线,可求得HF和FO,从而得解;
(3)可根据顶点位置的变动,得出抛物线y=-x2+4x右侧部分图象沿直线PH翻折后抛物线的解析式;由(2)FH直线解析式,平行于FH的直线l1:y=mx+t,其m值可求;令y=mx+t与翻折后抛物线相切,可求得t的临界值,结合图象可得最后答案.
解:(1)抛物线y=﹣x2+4x的对称轴为直线![]() .
.
∵点A的横坐标为1.代入y=﹣x2+4x得:y=3,
∴A(1,3),由抛物线的对称性得:点B的坐标为(3,3).
∴AB=2.
故答案为:2.
(2)∵B(3,3),E(1,1),
∴直线BE解析式为y=x,作l∥BE,且与抛物线相切,则可设l的解析式为:y=x+b.根据该直线与抛物线相切,列一元二次方程,令其判别式为0,可求得b的值,从而得点P的坐标,进而得点H坐标及PH长,
∴x+b=﹣x2+4x,即x2﹣3x+b=0,
∴△=9﹣4b=0,b=![]() ,
,
∴x2﹣3x+![]() =0,
=0,
∴切点为:x=![]() ,y=
,y=![]() ,
,
∴PH=![]() ﹣3=
﹣3=![]()
过点H作y=﹣x的垂线,交y=﹣x于点G,交y轴于点F,则GF=![]() FO,∠FGO=∠OFG=∠CFH=∠CHF=45°,
FO,∠FGO=∠OFG=∠CFH=∠CHF=45°,
![]()
![]()
![]() .
.
∴PH+HF+![]() FO的最小值为:
FO的最小值为:![]() .
.
(3)在(2)的条件下,平行于FH的直线l1:y=mx+t,若直线l1与函数M的图象有且只有2个交点,
∵∠CFH=45°,l1∥FH,
∴m=1,y=x+t,
∵抛物线y=﹣x2+4x的顶点D为(2,4),点H为(![]() ,3)点P为(
,3)点P为(![]() ,
,![]() ),
),
∴抛物线y=﹣x2+4x右侧部分图象沿直线PH翻折后抛物线顶点为(1,4),其解析式为y=﹣x2+2x+3.
当直线y=x+t与抛物线y=﹣x2+2x+3相切时,x+t=﹣x2+2x+3,
∴x2﹣x+t﹣3=0,△=1﹣4(t﹣3)=13﹣4t=0
∴t=![]() ;
;
∴t<![]() 时直线l1与函数M的图象有且只有2个交点.
时直线l1与函数M的图象有且只有2个交点.
∴t的取值范围为:t<![]() .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
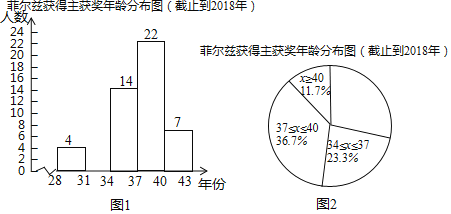
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.