题目内容
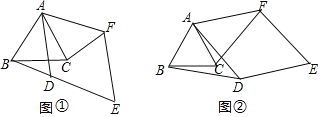
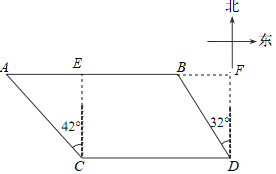
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

【答案】![]()
【解析】
过C作CE⊥AB于E,DF⊥AB交AB的延长线于F,于是得到CE∥DF,推出四边形CDFE是矩形,得到EF=CD=120,DF=CE,解直角三角形即可得到结论.
过C作CE⊥AB于E,DF⊥AB交AB的延长线于F,
则CE∥DF,
∵AB∥CD,
∴四边形CDFE是矩形,
∴EF=CD=120,DF=CE,
在Rt△BDF中,∵∠BDF=32°,BD=80,
∴DF=cos32°BD=80×![]() ≈68,BF=sin32°BD=80×
≈68,BF=sin32°BD=80×![]() ,
,
∴BE=EF-BF=![]() ,
,
在Rt△ACE中,∵∠ACE=42°,CE=DF=68,
∴AE=CEtan42°=68×![]() ,
,
∴AB=AE+BE=![]() +
+![]() ≈139m,
≈139m,
答:木栈道AB的长度约为139m.

 阅读快车系列答案
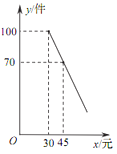
阅读快车系列答案【题目】重庆某大型车辆企业从去年开始出售“大鼻子安全校车”(以下简称校车).经统计发现,该校车月销售量P(辆)与月份x(1≤x≤12且x取整数)之间的函数关系如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 | … |
月销售量P(辆) | 66 | 68 | 70 | 72 | 74 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出P与x之间的函数关系式;
(2)若该校车在去年上半年的销售价格y1(万元)与月份x之间的函数关系式为y1=﹣0.5x+36(1≤x≤6且x取整数);去年下半年的销售价格y2(万元)与月份x之间的函数关系式为y2=﹣x+39(7≤x≤12且x取整数).此外,已知生产每辆校车的材料成本为12万元,人力和其他成本共4万元.问该企业去年哪个月销售校车的利润最大,并求出这个最大利润.