��Ŀ����
����Ŀ���Ѷ��Ƚ��ǹ��������г��������һ����ѧ���ÿ4����ѡһ�Σ��ڹ�����ѧ�Ҵ���ϰ����Խ�������䲻����40���������ѧ�ң������������ͩ1982���÷Ѷ��Ƚ���Ϊ����ѧ���˽�Ѷ��Ƚ�������������������Dz�ȡ�˽�ֹ��2018��60���Ѷ��Ƚ�������ʱ���������ݣ��������ݽ��������������ͷ�������������˲�����Ϣ��
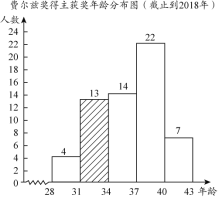
a����ֹ��2018��Ѷ��Ƚ�������ʱ���������ݵ�Ƶ���ֲ�ֱ��ͼ��ͼ1�����ݷֳ�5�飬������28��x��31��31��x��34��34��x��37��37��x��40��x��40����
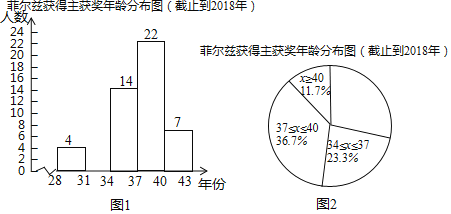
b����ͼ2����a�Ļ����ϣ���������ͳ��ͼ��
c����ֹ��2018��Ѷ��Ƚ�������ʱ��������34��x��37��һ��������ǣ�
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d����ֹ��2018��ʱ�Ѷ��Ƚ�������ʱ�������ƽ��������λ�����������£�
��� | ƽ���� | ��λ�� | ���� |
��ֹ��2018 | 35.58 | m | 37��38 |
����������Ϣ���ش��������⣺
��1���������⣬��ȫƵ��ֱ��ͼ��
��2��31��x��34�����Բ�ĽǶ����Ƕȣ�����ȫ����ͳ��ͼ��
��3��ͳ�Ʊ�����λ��m��ֵ�ǣ�
��4����������ͳ��ͼ���������Ѷ��Ƚ�������ʱ������ֲ�������
���𰸡���1����ͼ����������2��31��x��34�����Բ�ĽǶ����� 78�ȣ���ȫ����ͳ��ͼ����������3����λ��m��ֵ�� 36����4���𰸲�Ψһ���磺�Ѷ��Ƚ�������ʱ���伯����37����40�꣮
��������
��1������������Ϊ60����ڶ�����������ɽ������;
��2������Բ�Ľ�=360����ٷֱȼ��㼴�ɣ����ݰٷֱȵĺ�Ϊ1������ڶ���İٷֱȣ����ɻ�������ͳ��ͼ;
��3��������λ���Ķ��壬��λ�����ڵ�30��31�������ƽ����;
��4���𰸲�Ψһ���������ɣ�
��1����ͼ��
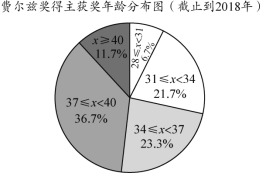
��2��31��x��34�����Բ�ĽǶ���=360���21.7%��78��;
��3����λ�����ڵ�30��31�������ƽ��������30��31������λ��34��x��37������2����Ϊ36,36����ͳ�Ʊ�����λ��m��ֵ�� 36��
��4���𰸲�Ψһ���磺�Ѷ��Ƚ�������ʱ���伯����37����40�꣮