题目内容
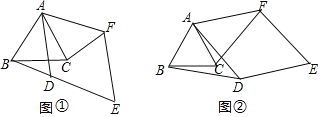
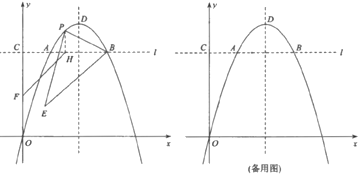
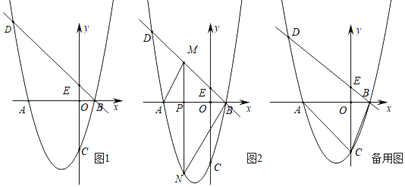
【题目】如图1,直线1:y=﹣x+1与x轴、y轴分别交于点B、点E,抛物线L:y=ax2+bx+c经过点B、点A(﹣3,0)和点C(0,﹣3),并与直线l交于另一点D.
(1)求抛物线L的解析式;
(2)点P为x轴上一动点
①如图2,过点P作x轴的垂线,与直线1交于点M,与抛物线L交于点N.当点P在点A、点B之间运动时,求四边形AMBN面积的最大值;
②连接AD,AC,CP,当∠PCA=∠ADB时,求点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)①S四边形AMBN最大值为![]() ;②P的坐标:P1
;②P的坐标:P1![]() ,P2(﹣15,0).
,P2(﹣15,0).
【解析】
(1)先求出B的坐标,再将A、B、C坐标代入y=ax2+bx+c列方程组,然后求解,即可求出抛物线的解析式;
(2)①根据S四边形AMBN=![]() ABMN=
ABMN=![]() =﹣2(x+
=﹣2(x+![]() )2+
)2+![]() ,所以当x=﹣
,所以当x=﹣![]() 时,S四边形AMBN最大值为
时,S四边形AMBN最大值为![]() ;
;
②先联立方程组.求出D点的坐标,两种情况讨论:Ⅰ.当点P在点A的右边,∠PCA=∠ADB时,△PAC∽△ABD;Ⅱ.当点P在点A的左边,∠PCA=∠ADB时,记此时的点P为P2,则有∠P2CA=∠P1CA.
(1)∵y=﹣x+1,
∴B(1,0),
将A(﹣3,0)、C(0,﹣3),B(1,0)代入y=ax2+bx+c,
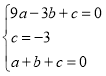 ,
,
∴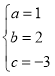
∴抛物线L的解析式:y=x2+2x﹣3;
(2)设P(x,0).
①S四边形AMBN=![]() ABMN
ABMN
=![]()
=﹣2(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,S四边形AMBN最大值为
时,S四边形AMBN最大值为![]() ;
;
②由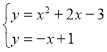 ,得
,得 ,
,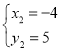 ,
,
∴D(﹣4,5),
∵y=﹣x+1,
∴E(0,1),B(1,0),
∴OB=OE,
∴∠OBD=45°.
∴BD=![]() .
.
∵A(﹣3,0),C(0,﹣3),
∴OA=OC,AC=![]() ,AB=4.
,AB=4.
∴∠OAC=45°,∴∠OBD=∠OAC.
Ⅰ.当点P在点A的右边,∠PCA=∠ADB时,△PAC∽△ABD.
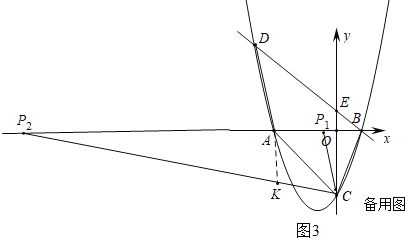
∴![]() ,
,
∴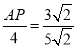 ,
,
∴![]() ,
,
∴P1![]()
Ⅱ.当点P在点A的左边,∠PCA=∠ADB时,记此时的点P为P2,则有∠P2CA=∠P1CA.
过点A作x轴的垂线,交P2C于点K,则∠CAK=∠CAP1,又AC公共边,
∴△CAK≌△CAP1(ASA)
∴AK=AP1=![]() ,
,
∴K(﹣3,﹣![]() ),
),
∴直线CK:![]() ,
,
∴P2(﹣15,0).
P的坐标:P1![]() ,P2(﹣15,0).
,P2(﹣15,0).

 阅读快车系列答案
阅读快车系列答案【题目】重庆某大型车辆企业从去年开始出售“大鼻子安全校车”(以下简称校车).经统计发现,该校车月销售量P(辆)与月份x(1≤x≤12且x取整数)之间的函数关系如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 | … |
月销售量P(辆) | 66 | 68 | 70 | 72 | 74 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出P与x之间的函数关系式;
(2)若该校车在去年上半年的销售价格y1(万元)与月份x之间的函数关系式为y1=﹣0.5x+36(1≤x≤6且x取整数);去年下半年的销售价格y2(万元)与月份x之间的函数关系式为y2=﹣x+39(7≤x≤12且x取整数).此外,已知生产每辆校车的材料成本为12万元,人力和其他成本共4万元.问该企业去年哪个月销售校车的利润最大,并求出这个最大利润.