题目内容
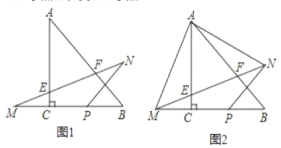
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与B.C重合)点P关于直线AC、AB的对称点分别为M、N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值
(2)当点P在线段BC上运动时(不与B.C重合),连接AM、AN,求证:
①△AMN为等腰直角三角形
②△AEF∽△BAM
【答案】(1)![]() ;(2)证明见解析;
;(2)证明见解析;
【解析】
(1)连接NB,如图1,先由△ACB为等腰直角三角形得到∠A=∠CBA=45°,则根据对称的性质得AB垂直PN,BN=BP,则∠NBA=∠PBA=45°,所以∠PBN=90°,接着计算出MC=CP=PB=NB=1,然后利用正切的定义求解
(2)①连接AP,如图2,利用对称的性质得AP=AM=AN,∠1=∠2,∠3=∠4,则∠MAN=90°,于是可判断△AMN为等腰直角三角形
②利用△AMN为等腰直角三角形得到∠5=∠6=45°,再证明∠AEF=∠BAM,加上∠B=∠EAF=45°,则根据相似三角形的判定可判断△AEF∽△BAM
(1)连接NB,如图1
∵在Rt△ABC中,∠ACB=90°,AC=BC
∴△ACB为等腰直角三角形,
∴∠A=∠CBA=45°
∵点P关于直线AB的对称点为,关于直线AC的对称点为M,
∴AB垂直PN,BN=BP
∴∠NBA=∠PBA=45°
∴∠PBN=90°,
∵点P为BC的中点,BC=2,
∴MC=CP=PB=NB=1
∴tan∠M=![]()
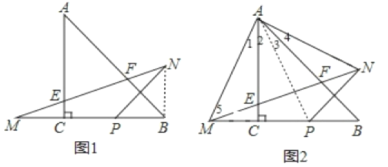
(2)证明:①连接AP,如图2,
∵点P关于直线AC、AB的对称点分别为M、N
∴AP=AM=AN,∠1=∠2,∠3=∠4
∴∠CAB=∠2+∠3=45°
∴∠MAN=90°
∴△AMN为等腰直角三角形
②∵△AMN为等腰直角三角形
∴∠5=∠6=45°
∴∠AEF=∠5+∠1=45°+∠1,
∵∠EAF=45°
∴∠BAM=∠EAF+∠1=45°+∠1
∴∠AEF=∠BAM,
又∵∠B=∠EAF=45°
∴△AEF∽△BAM

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】2019年永州市初中体育水平测试进行改革,增加了自选项目,学生可以从篮球运球、足球运球、排球向上垫球三项中必须选一项,另外从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远中必须选一项.现对永州市某校的选考项目情况进行调查,对调查结果进行了分析统计并制作了两幅统计图:
项目 | 篮球 | 足球 | 排球 | |||
性别 | 男 | 女 | 男 | 女 | 男 | 女 |
人数 | 30 | 10 | 24 | 12 | 6 | 28 |
平均得分 | 8 | 7 | 8.5 | 6 | 9 | 10 |
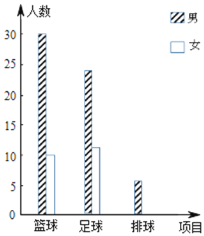
(1)补全条形统计图;
(2)求抽查的这些男生的体育测试平均分;
(3)若该校准备从这次体育测试成绩好的学生中选出10名参加全市运动会.现在有19名学生报名,小明是这19名同学之一,小明在知道自己这次成绩后还需知道这19名学生成绩的______,就能知道自己能不能参加市运动会.
A.平均数B.众数C.中位数D.方差
【题目】重庆某大型车辆企业从去年开始出售“大鼻子安全校车”(以下简称校车).经统计发现,该校车月销售量P(辆)与月份x(1≤x≤12且x取整数)之间的函数关系如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 | … |
月销售量P(辆) | 66 | 68 | 70 | 72 | 74 | … |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出P与x之间的函数关系式;
(2)若该校车在去年上半年的销售价格y1(万元)与月份x之间的函数关系式为y1=﹣0.5x+36(1≤x≤6且x取整数);去年下半年的销售价格y2(万元)与月份x之间的函数关系式为y2=﹣x+39(7≤x≤12且x取整数).此外,已知生产每辆校车的材料成本为12万元,人力和其他成本共4万元.问该企业去年哪个月销售校车的利润最大,并求出这个最大利润.