Question

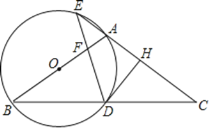
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC，垂足为点H，连接DE，交AB于点F．

（1）求证：DH是⊙O的切线；

（2）若⊙O的半径为4，

①当AE＝FE时，求 的长（结果保留π）；

②当 时，求线段AF的长．

Answer 1

【答案】（1）详见解析；（2）①；②

【解析】

（1）根据同圆的半径相等和等边对等角证明：∠ODB＝∠OBD＝∠ACB，则DH⊥OD，DH是圆O的切线；

（2）①根据等腰三角形的性质的∠EAF＝∠EAF，设∠B＝∠C＝α，得到∠EAF＝∠EFA＝2α，根据三角形的内角和得到∠B＝36°，求得∠AOD＝72°，根据弧长公式即可得到结论；

②连接AD，根据圆周角定理得到∠ADB＝∠ADC＝90°，解直角三角形得到AD＝，根据相似三角形的性质得到AH＝3，于是得到结论．

证明：（1）连接OD，如图，

∵OB＝OD，

∴△ODB是等腰三角形，

∠OBD＝∠ODB①，

在△ABC中，∵AB＝AC，

∴∠ABC＝∠ACB②，

由①②得：∠ODB＝∠OBD＝∠ACB，

∴OD∥AC，

∵DH⊥AC，

∴DH⊥OD，

∴DH是圆O的切线；

（2）①∵AE＝EF，

∴∠EAF＝∠EAF，

设∠B＝∠C＝α，

∴∠EAF＝∠EFA＝2α，

∵∠E＝∠B＝α，

∴α+2α+2α＝180°，

∴α＝36°，

∴∠B＝36°，

∴∠AOD＝72°，

∴的长＝；

②连接AD，

∵AB为⊙O的直径，

∴∠ADB＝∠ADC＝90°，

∵⊙O的半径为4，

∴AB＝AC＝8，

∵，

∴，

∴AD＝，

∵AD⊥BC，DH⊥AC，

∴△ADH∽△ACD，

∴，

∴，

∴AH＝3，

∴CH＝5，

∵∠B＝∠C，∠E＝∠B，

∴∠E＝∠C，

∴DE＝DC，∵DH⊥AC，

∴EH＝CH＝5，

∴AE＝2，

∵OD∥AC，

∴∠EAF＝∠FOD，∠E＝∠FDO，

∴△AEF∽△ODF，

∴，

∴，

∴AF＝．