题目内容
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2)![]() ,
,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)根据“等差”函数的定义,可知![]() ,
,![]() ,列方程求出b的值即可;
,列方程求出b的值即可;
(2)根据“等差”函数的定义可得![]() ,
,![]() ,由此可列出“等差”函数的解析式和反比例函数的解析式,当
,由此可列出“等差”函数的解析式和反比例函数的解析式,当![]() 时联立两函数解析式可求出
时联立两函数解析式可求出![]() ,问题得解;
,问题得解;
(3)根据“等差”函数的定义用c表示出a和b,然后得到“等差”函数的解析式与一次函数解析式,求出![]() 的值,过点P
的值,过点P![]() 作
作![]() 轴,交AB于H,求出
轴,交AB于H,求出![]() ,然后根据三角形面积公式和二次函数的最值求解.
,然后根据三角形面积公式和二次函数的最值求解.
解:(1)存在.
假设一次函数![]() 与反比例函数
与反比例函数![]() 存在“等差”函数,
存在“等差”函数,
则![]() ,
,![]() ,
,![]()
解得:![]()
![]() 存在“等差”函数,其解析式为
存在“等差”函数,其解析式为![]() ;
;
(2)根据题意知:![]() ,
,![]()
![]()
则“等差”函数的解析式为![]() ,
,
反比例函数的解析式为![]()
根据题意,将![]() 代入
代入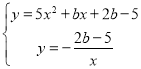 ,
,
得:![]() ,解得
,解得![]() ,
,![]()
故一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ;
;
(3)存在.
根据题意知:![]() ,
,![]()
![]() ,
,![]()
则“等差”函数的解析式为![]() ,一次函数解析式为
,一次函数解析式为![]()
![]()
![]() 与“等差”函数
与“等差”函数![]() 有两个交点
有两个交点![]() ,
,
![]()
![]() 即
即![]()
![]()
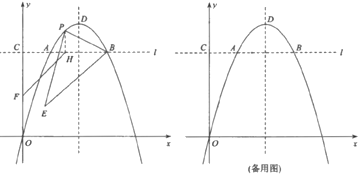
如图,过点P![]() 作
作![]() 轴,交AB于H,
轴,交AB于H,
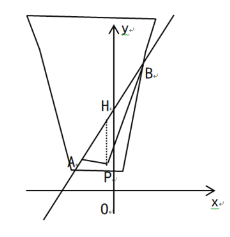
![]()
![]() 点
点![]()
![]()
![]()
![]() 点在
点在![]() ,
,![]() 之间
之间![]()
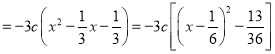
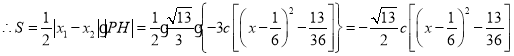
![]() 当
当![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案