ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΒψPΘ®x0Θ§y0Θ©ΚΆ÷±œΏyΘΫkx+bΘ§‘ρΒψPΒΫ÷±œΏyΘΫkx+bΒΡΨύάκdΩ…”ΟΙΪ ΫdΘΫ![]() ΦΤΥψΘ°
ΦΤΥψΘ°
άΐ»γΘΚ«σΒψPΘ®©¹2Θ§1Θ©ΒΫ÷±œΏyΘΫx+1ΒΡΨύάκΘ°
ΫβΘΚ“ρΈΣ÷±œΏyΘΫx+1Ω…±δ–ΈΈΣx©¹y+1ΘΫ0Θ§Τδ÷–kΘΫ1Θ§bΘΫ1Θ°
Υυ“‘ΒψPΘ®©¹2Θ§1Θ©ΒΫ÷±œΏyΘΫx+1ΒΡΨύάκΈΣdΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ°
Θ°
ΗυΨί“‘…œ≤ΡΝœΘ§«σΘΚ
Θ®1Θ©ΒψPΘ®2Θ§4Θ©ΒΫ÷±œΏyΘΫ3x©¹2ΒΡΨύάκΘ§≤ΔΥΒΟςΒψP”κ÷±œΏΒΡΈΜ÷ΟΙΊœΒΘΜ
Θ®2Θ©ΒψPΘ®2Θ§1Θ©ΒΫ÷±œΏyΘΫ2x©¹1ΒΡΨύάκΘΜ
Θ®3Θ©“―÷Σ÷±œΏyΘΫ©¹3x+1”κyΘΫ©¹3x+3ΤΫ––Θ§«σ’βΝΫΧθ÷±œΏΒΡΨύάκΘ°
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈωΘΜ(2)![]() ;(3)
;(3)![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί“―÷ΣΒΡΨύάκΙΪ ΫΦ¥Ω…«σΒψΒΫ÷±œΏΒΡΨύάκΘ§¥”ΕχΥΒΟςΒψP”κ÷±œΏΒΡΈΜ÷ΟΙΊœΒΘΜ
Θ®2Θ©ΗυΨί“―÷ΣΒΡΨύάκΙΪ ΫΦ¥Ω…«σΫβΘΜ
Θ®3Θ©‘Ύ“―÷ΣΒΡ“ΜΧθ÷±œΏ…œ»Γ“ΜΒψΘ§‘ΌΗυΨίΒψΒΫ÷±œΏΒΡΨύάκΙΪ ΫΦ¥Ω…«σΒΟΫα¬έΘ°
Θ®1Θ©ΓΏΒψPΘ®2Θ§4Θ©Θ§
ΓύΒψPΒΫ÷±œΏyΘΫ3x©¹2ΒΡΨύάκΈΣΘΚdΘΫ![]() ΘΫ0Θ°
ΘΫ0Θ°
ΓύΒψP‘Ύ÷±œΏyΘΫ3x©¹2…œΘ°
¥πΘΚΒψPΒΫ÷±œΏyΘΫ3x©¹2ΒΡΨύάκΈΣ0Θ§ΒψP‘Ύ÷±œΏyΘΫ3x©¹2…œΘ°
Θ®2Θ©ΓΏΒψPΘ®2Θ§©¹1Θ©
ΓύΒψPΒΫ÷±œΏyΘΫ2x©¹1ΒΡΨύάκΈΣΘΚdΘΫ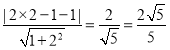 Θ°
Θ°
¥πΘΚΒψPΒΫ÷±œΏyΘΫ2x©¹1ΒΡΨύάκΈΣ![]() Θ°
Θ°
Θ®3Θ©‘Ύ÷±œΏyΘΫ©¹3x+1»Έ“β»Γ“ΜΒψPΘ§Β±xΘΫ0 ±Θ§yΘΫ1Θ°
ΓύPΘ®0Θ§1Θ©Θ°
ΓύΒψPΒΫ÷±œΏyΘΫ©¹3x+3ΒΡΨύάκΈΣΘΚdΘΫ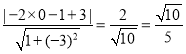 Θ°
Θ°
¥πΘΚΝΫΤΫ––œΏ÷°ΦδΒΡΨύάκΈΣ![]() Θ°
Θ°

ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐ![]() ΒΡ
ΒΡ![]() ”κ
”κ![]() ΒΡ≤ΩΖ÷Ε‘”Π÷Β»γ±μΘΚ
ΒΡ≤ΩΖ÷Ε‘”Π÷Β»γ±μΘΚ
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
œ¬Ν–Ϋα¬έΘΚΔΌ≈ΉΈοœΏΒΡΩΣΩΎœρ…œΘΜΔΎ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ÷±œΏ![]() ΘΜΔέΒ±
ΘΜΔέΒ±![]() ±Θ§
±Θ§![]() ΘΜΔή3 «ΖΫ≥Χ
ΘΜΔή3 «ΖΫ≥Χ![]() ΒΡ“ΜΗωΗυΘΜΔί»τ
ΒΡ“ΜΗωΗυΘΜΔί»τ![]() Θ§
Θ§![]() «≈ΉΈοœΏ…œΝΫΒψΘ§‘ρ
«≈ΉΈοœΏ…œΝΫΒψΘ§‘ρ![]() Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
A.1B.2C.3D.4