题目内容
【题目】如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.
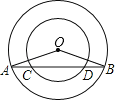
(1)求证AC=BD;
(2)若AC=3,大圆和小圆的半径分别为6和4,则CD的长度是 .
【答案】(1)见解析;(2)![]()
【解析】
(1)作CH⊥CD于H,如图,根据垂径定理得到CH=DH,AH=BH,利用等量减等量差相等可得到结论;
(2)连接OC,如图,设CH=x,利用勾股定理得到OH2=OC2﹣CH2=42﹣x2,OH2=OA2﹣AH2=62﹣(3+x)2,则42﹣x2=62﹣(3+x)2,然后解方程求出x即可得到CD的长.
(1)作CH⊥CD于H,如图,∵OH⊥CD,∴CH=DH,AH=BH,∴AH﹣CH=BH﹣DH,∴AC=BD;
(2)连接OC,如图,设CH=x.在Rt△OCH中,OH2=OC2﹣CH2=42﹣x2.在Rt△OAH中,OH2=OA2﹣AH2=62﹣(3+x)2,∴42﹣x2=62﹣(3+x)2,解得:x=![]() ,∴CD=2CH=
,∴CD=2CH=![]() .
.

练习册系列答案
相关题目